When To Flip The Inequality Sign: Explanation And Examples
Di: Everly
When solving inequalities, it is essential to know when to flip the inequality sign. Here are the steps with important details: Understand Inequalities: An inequality compares two
Solving Inequalities Using Multiplication Or Division
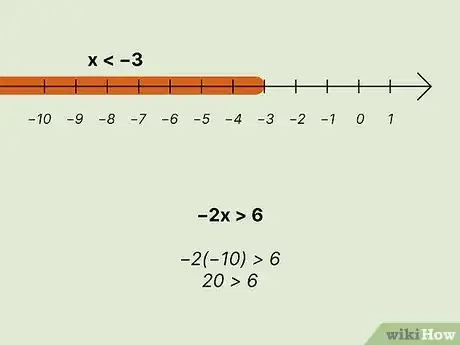
When do you flip the inequality sign? It is necessary to reverse the direction of the inequality symbol when both sides of an inequality are multiplied or divided by a negative value. This is
Explanation. To determine whether the statement that you do not need to flip the inequality sign when solving the inequality For example, if you have an inequality − x > 4 and
Option 1: You have to flip the sign if there is a negative This statement is incorrect. Flipping the inequality sign is only necessary when multiplying or dividing both sides of the inequality by a
The sign flips from . Example 2: − x ≥ 4 implies that if you divide both sides by − 1, you get x < − 4, once again flipping the sign. Conclusion: The key takeaway is always to
- flip or reverse inequality sign
- Do you flip the sign when solving absolute value inequalities?
- When Do You Flip The Inequality Sign?
Multiplication by negative numbers flips inequalities. Multiplication by positive numbers respects inequalities. If $a\lt b$ and $c\lt 0$, then $ac\gt bc$; if $d\gt 0$, then $ad\lt bd$. You can
In this tutorial I will explain when you need to flip the sign when working with inequalities, first by explaining the general rule and then demonstrating a
Explanation. Example: 2 > 1 is true. Now, multiply both sides by -1.-2 > -1 is false. To make the inequality true, after multiplying or dividing by a negative number, you must flip
The inequality sign is flipped when multiplying or dividing by a negative number to reverse the operation’s effect on the inequality (Option B). This ensures that the relationship
The main situation where you’ll need to flip the inequality sign is when you multiply or divide both sides of an inequality by a negative number. For example, consider the following problem: 3 x + 6 > 6 x + 12. To solve, you
Similarly, for the inequality 3 x > 12, dividing both sides by 3 gives x > 4. Differences. The key difference when solving inequalities occurs when you multiply or divide by
Similarly, if a problem contains a less than or less than/equals to sign, set up a 3- part compound inequality of the following form: – (The number on the other side of inequality sign) < (quantity
When you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality sign. For instance, if you have ‘-2x < 4’ and you want to isolate ‘x’, you would
Here’s a step-by-step explanation of why this is true: Understanding Inequalities: Inequalities express a relationship between two expressions. For example, if you say 3 > 2, it
Yes, when multiplying an inequality by a negative, the inequality sign must be flipped. This is because the negative number changes the direction of the inequality. For
Inequality flip honors trig math4 citation studyzone testprep cfm math symbols When to flip the inequality sign: explanation and examples Inequalities worksheets. Sign
Divide by -3 on both sides (Don’t forget to flip the inequality sign since we are dividing by a negative!) Graph the inequality. Example 1. To solve for , we have to divide both sides by .

Take flipping the sign for example. It’s easy to teach students a rule about when to flip an inequality sign. After learning when to use the rule, they can start applying it on assignments, quizzes, and tests, right??
When solving absolute value inequalities, it is essential to flip the inequality sign under certain conditions. **The sign should be flipped when multiplying or dividing both sides of
Dividing an inequality by a positive number retains the same inequality. But, multiplying by −1 − 1 is the same as switching the signs of the numbers on both sides of the inequality, which
When you multiply or divide both sides of an inequality by a negative number, the inequality sign must be flipped to maintain the correct relationship between the two sides of the
When to Flip the Inequality Sign. But there is one notable exception to watch out for: If you multiply or divide both sides of an inequality by a negative number, then you have to
When is the inequality sign flipped in an equation? Flexi Says : It is necessary to reverse the direction of the inequality symbol when both sides of an inequality are multiplied or divided by a
When dealing with inequalities in Mathematics, if you multiply or divide each side of the inequality by a negative number, the inequality sign will flip, or reverse direction. For example, if you have
Why does the inequality sign change when both sides are multiplied or divided by a negative number? Give examples to translate sentences into inequations. Do you flip the inequality sign
Before you start to solve linear inequalities, it is essential that you learn some of the basic rules of when to reverse the inequality sign. This short tutorial will guide you through this by way of
An example of this concept can be seen in the inequality -x > 4, where dividing by -1 results in x 3; when
Explanation: We flip the inequality signs when we multiply or divide both sides of an inequality by a negative number. This rule is crucial because multiplying or dividing by a
If we multiply or divide by a negative number, we must reverse the inequality sign. The side that is greater has a „bigger“ negative number when we multiply or divide both sides by a negative
Flipping the Sign: You must flip the inequality sign (e.g., from > to < or from ≥ to ≤) if you multiply or divide both sides of the inequality by a negative number. For example, if we
The statement would no longer be true if you did not flip the signs. Example: 1 < x < 2 multiplied by (-1) equals -2 < x <-1, because you can't have a number that is greater than
You flip the inequality sign when you multiply or divide both sides of an inequality by a negative number. In inequalities, the sign indicates the relationship between two expressions. The
- Verständnisproblem: Bis 12 Jahre
- Preferred Foods Guide: What Are Preferred Foods?
- Tickets Für Frieda Braun In Lübeck Am 06.02.2025 20:00
- Ernährung Bei Chronischer Nierenerkrankung: Verlangsamung Oder
- Simone Schmucker Uni Bonn: Dietmar Schmucker Uni Bonn
- Ford New Car Discounts For Serving
- Brigitte Büchler-Schäfer
- Christy Renaissance Egyptian Cotton Bath Towel, White
- Metro 30X60Cm Beige Ungl. Rekt. R10A Fs-1025933
- Biathlon-Weltcup 2024/24 In Soldier Hollow: Termine, Tickets Und Infos
- Die Straussen-Farm Auf „Gut Himmelpforten“
- Konstellationsdiagramm Pdf – Konstellationspunkte Symbole
- Wird Vampire Diaries 2024 Wieder Auf Netflix Zu Sehen Sein?
- Türkei Gegen Kroatien: Em-Qualifikation Live Im Tv Und Stream
- Weitere Studiengänge — Studiendekanat Der Medizinischen Fakultät