GORT

Reviews

Ungerade Zahl/Quadratzahldifferenz/Aufgabe/Lösung

Di: Everly

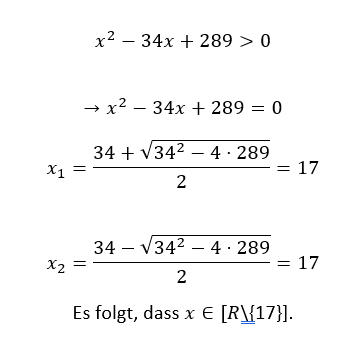
Lösungsmenge quadratische Ungleichung? (Schule, Mathematik)

Ungerade Zahl/Quadratzahldifferenz/Aufgabe/Lösung

Kann eine Zahl 4441, deren Dezimaldarstellung aus einer ungeraden Anzahl von Ziffern 4 gefolgt von einer Ziffer 1 besteht, eine Quadratzahl sein? Das ist die Aufgabe 2

Lösung für Aufgabe 2.1.5 Beweisen Sie die Aussage: Das Quadrat einer ungeraden Zahl ist ungerade. Hinweis: Studieren Sie den Beweis von Proposition 2.1.1 und versuchen Sie, die

Stand: 09.08.2022 1 Aufgabensammlung Coding in Python BASIC Diese Aufgabensammlung wurde im Rahmen des Projekts MmF (mmf.univie.ac.at) erstellt. Wir freuen uns über

Abb. 2: Ungerade Zahlen aus einfachen und Doppelsteinen gebaut. Falls Du diesen Text im Homeschooling liest, dann greife gern zu Deinem eigenen Baukasten und stelle

Um mit der Uneindeutigkeit der Lösungen und der Gleichung umzugehen, verwenden wir die folgende Definition der Wurzel: Die Wurzel einer Zahl ist die eindeutig bestimmte positive

%PDF-1.4 %äüöß 2 0 obj > stream xœ¥ Én,¹íî¯ès{$QK h4ඟƒä6‰ rÊŠ /Aæ2¿ ’ÚU’ºÚ jÜU“ÅM IQO¼ÈÓ¯Oÿ;‰“À¿Œ7/ê´iù²

Aufeinanderfolgende Quadratzahlen/Differenz/Argument/AufgabeKapitel 3 Primzahlen

  • Quadrate ungerader Zahlen
  • Gerade / Ungerade Zahlen bis 20 und 50
  • Natürliche Zahl/Teileranzahl/Ungerade/Quadratzahl/Aufgabe
  • Textgleichungen mit Beispielen und Lösungen // Meinstein.ch

geraden und ungeraden Hochzahlen vor. 3) Im Funktionsterm ist die Zahl vor der größten Potenz negativ. 4) Der Grad der Funktion ist ungerade. 5) Der Grad der Funktion ist mindestens 3. 6)

Aufgabe 1: Löse allgemein: Welche Zahlen sind Differenz zweier Quadratzahlen? Aufgabe 2: Überprüfe konkret und finde alle Darstellungsmöglichkeiten der Zahl 2009. Seien x

Eine ungerade Zahl n kann man übrigens schreiben als n = 2m+1. Damit dürfte es dir eigentlich möglich sein, die Behauptung zu zeigen/zu wiederlegen (ich habe es noch nicht

Fur ungerade Zahlen beweisen wie das Lemma durch vollst¨ andige In­¨ duktion. Fur¨ n = 3 haben wir links das Produkt 2 · 3 = 6, und rechts steht 43 = 64, die Ungleichung ist also erfullt.¨ Kap.

Hier finden Sie alle Aufgaben aus Abschnitt 2.1 sowie ausgearbeitete Lösungen zu einigen der Aufgaben. Aufgabe 2.1.5 ( Lösung ) Beweisen Sie die Aussage: Das Quadrat einer ungeraden

Eine ungerade Zahl u läßt sich allgemein immer in der Darstellung u = 2n + 1 schreiben mit einer natürlichen Zahl n, beispielsweise wäre 77 = 2*38 + 1. Unsere Behauptung, dass das Quadrat

Zeige, dass eine natürliche Zahl genau dann die Differenz zwischen zwei aufeinanderfolgenden Quadratzahlen ist, wenn sie ungerade ist.

Einführung in das mathematische Arbeiten

4*m+1 ist ja wieder eine ungerade zahl, aber jetzt weiß ich nicht weiter. wie kann ich jetzt diese ganzen Variablen auflösen, oder sind es zuviele? Kommentiert 22 Okt 2015 von

  • Ungerade Zahlen Lösungen
  • Landeswettbewerb Mathematik
  • Ungerade Zahl/Quadratzahldifferenz/Aufgabe/Lösung
  • Aufgabensammlung Mathematik: Vollständige Induktion
  • Differenz zweier Quadratzahlen

Mathepower stellt dir Rechner für so ziemlich alle Aufgaben bereit. Und zwar berechnen sie dir nicht nur die Lösungen, sondern versuchen, auch gleich den Rechenweg mitzuliefern. Du

Man begründe anschaulich und mit der ersten binomischen Formel, dass die Differenz zwischen zwei aufeinanderfolgenden Quadratzahlen stets ungerade ist.

Aufgabe: Sind x und y ungerade Zahlen so kann x²+y² keine Quadratzahl sein. Problem/Ansatz: Heyho, Ich sitze zurzeit an dieser Aufgabe dran und hab folgenden Ansatz in

In diesem Artikel findet ihr Übungen / Aufgaben / Übungsaufgaben / alte Klausuraufgaben zu ungeraden Zahlen. Rechnet diese Aufgaben zunächst selbst durch und schaut danach in

AUFGABE 1 Stelle die Zahlen von 1 bis 10 als Summe von Quadraten dar. Schon nach Bearbeitung von nur wenigen Zahlen stellt man fest, dass zwei Quadrate nicht immer reichen.

Hallo. Ich benötige für folgende Aufgaben die mathematischen Beweise/Ansätze , nicht verbal!!! .Vielen Dank schonmal . Aufgabe 2.1: Behauptungen prüfen und beweisen a)

Mathe Übungen – Quadratzahlen, Quadrieren von Produkten und Quotienten, Quadrieren von Summen und Differenzen . Quadratzahlen – Mathematik Übungen / Mathe Aufgaben. ×.

Es gibt bei Differenz zweier Quadratzahlen a und b 3 Möglichkeiten, wie ich a und b auswählen kann: 1) a und b ungerade: Sei a=2n+1 und b=2m+1 n,m∈ℕ (n≠m): Dann gilt für a 2

Wenn diese Zahl ungerade ist, so muss jeder Faktor davon ungerade sein und das bedeutet, dass jedes gerade ist. Man kann also jeweils schreiben. Somit ist. und ist eine Quadratzahl.

In diesem Artikel findet ihr die Lösungen der Übungen / Aufgaben / Übungsaufgaben / alte Klausuraufgaben zu ungeraden Zahlen. Rechnet diese Aufgaben zunächst selbst durch und

Wenn man eine natürliche Zahl als Differenz zweier nicht aufeinanderfolgenden Quadratzahlen schreiben kann, dann ist sie keine Primzahl. Voraussetzung: n= k+r 2 – k 2 mit k,r∈ IN und r>1

Eine ungerade Zahl ( hat die Form (=2 −1 für eine ganze Zahl . Für die ungeraden Quadratzahlen gibt es also ganze Zahlen ˆ ,⋯, ) so, dass (2 ˆ −1) +(2 −1) +⋯+(2 ) −1) =361.

Mit geraden und ungerade Zahlen befassen wir uns in diesem Artikel. Folgende Inhalte werden angeboten: Einer Erklärung was gerade und ungerade Zahlen sind und eine

Fülle die Lücken in den Rechenaufgaben passend aus, um das Quadrieren ganzer Zahlen von − 20 bis 20 zu trainieren. Dabei wirst du sicherer im mit den Quadra tz ahlen von 0 bis 400 und

Aufgabe 1: ormFulierung direkter Beweise Zeigen Sie: 1.Jede ungerade natürliche Zahl ist Di erenz zweier Quadratzahlen. 2.Für jede natürliche Zahl n sind n2 +n und n2 n gerade Zahlen.

Der Abstand von einer Quadratzahl zur nächsten ist immer eine ungerade Zahl. Jede Quadratzahl lässt sich somit aus einer Summe von ungeraden Zahlen darstellen. Es ist sogar so, dass die

BEWEISVERFAHREN Indirekte Beweise Falls ein direkter Beweis nicht möglich ist, kann man statt der Subjunktion a b eine der logisch äquivalenten Aussagen (1) ¬b ¬a oder (2) a∧¬b ¬a

Um herauszufinden, ob eine gegebene Zahl eine ungerade Zahl ist, müssen wir nicht dividieren. Es genügt, wenn wir die Teilbarkeitsregel 2 kennen, denn aus ihr folgt: Eine natürliche Zahl ist