Special Functions
Di: Everly
A comprehensive and authoritative reference on special functions in mathematics, covering topics such as gamma, beta, hypergeometric, Bessel, orthogonal, and q-series. The book provides definitions, properties, identities, applications, and
Videos von Special functions
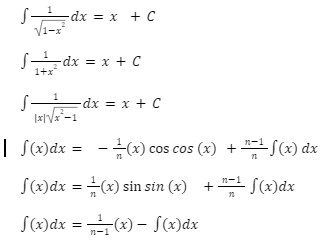
A comprehensive reference book on special functions, their derivatives, integrals, series and other formulas. Covers elementary, Bessel, hypergeometric, elliptic, Airy, Legendre, Chebyshev,
Wikimedia Commons has media related to Special functions. The main article for this category is Special functions. This category has the following 8 subcategories, out of 8 total. The following
The special functions of mathematical physics are those functions that play a key role in many problems in science and engineering. For example, Bessel, Legendre, or
Chapter 1 introduces elementary classical special functions. Gamma, beta, psi, zeta functions, hypergeometric functions and the associated special functions, gen-eralizations to Meijer’s G
Special functions, being natural generalizations of the elementary functions, have their origin in the solution of partial differential equations satisfying some set of conditions. Special functions
- Notes on Special Functions
- Videos von Special functions
- Category:Special functions
Special functions are important objects in both mathematics and physics. First we introduce the gamma function Γ ( z ) as a continuous generalization of n ! and prove the beta function
Special Functions and Orthogonal Polynomials
Special mathematical functions. The naming and numbering of the functions is taken from Matt Austern, (Draft) Technical Report on Standard Library Extensions, N1687=04-0127, September
Abstract. Special functions are essential for solving problems in virtually all engineering disciplines. Assuming only knowledge of elementary calculus and differential
Special functions are mathematical functions that have established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other
Learn about Bessel functions, the gamma function, and Legendre polynomials, and how they arise in problems with circular or spherical symmetry. See examples, definitions, series,
A comprehensive overview of various types of functions in mathematics, with definitions, examples, and applications. Includes elementary, transcendental, special, and piecewise
Functions that occur frequently, and are therefore useful, are often called special functions. In many cases, special functions are solutions of ordinary or partial differential equations or of
Encyclopedia of Special Functions: The Askey-Bateman Project
Airy Functions: besselh: Bessel function of third kind (Hankel function) besseli: Modified Bessel function of first kind: besselj: Bessel function of first kind: besselk: Modified Bessel function of
special functions during the past twenty-three years. It is my hope, however, that Asymptotics and Special Functions will continue to provide a useful broad introduction as well as a work of
Special Functions a(j+1)=j*a(j) enddo 1 1 ntop=n factrl=a(n+1) else Larger value than size of table is required. Actually, this big a value is going to over ow on many computers, but no harm in
Special functions are mathematical functions that have established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other
Where Γ = the gamma function.. Each G-function is a linear combination of special functions. These include as special cases: Higher transcendental hypergeometric functions, All four
The Handbook of Special Functions provides in-depth coverage of special functions, which are used to help solve many of the most difficult problems in physics, engineering, and mathematics.
Special functions (scipy.special)# Almost all of the functions below accept NumPy arrays as input arguments as well as single numbers. This means they follow broadcasting and automatic
Products and services. Our innovative products and services for learners, authors and customers are based on world-class research and are relevant, exciting and inspiring.
Special Functions Muzammil Tanveer [email protected] 0316-7017457 . Collected by: Muhammad Saleem Composed by: Muzammil Tanveer 1 Dedicated To My Honorable Teacher
the newly established special functions involving the Mittag-Leffler, Wiman, Prab-hakar, Miller–Ross, Rabotnov, Lorenzo–Hartley, Sonine, Wright, and Kohlrausch– Williams–Watts
Special Functions GEORGE E. ANDREWS RICHARD ASKEY RAN JAN ROY CAMBRIDGE UNIVERSITY PRESS. Contents Preface page xiii 1 The Gamma and Beta Functions 1 1.1 The
SPECIAL FUNCTIONS – Ira A. Fulton College of Engineering
This chapter is devoted primarily to the classical orthogonal polynomials, although a final section also discusses the Bessel functions of the first kind. We are for the most part interested in the
- Aufgaben Des Taufpaten: Das Müssen Sie Wissen
- Ein Master Als Türöffner Für Die Karriere
- Müssen Meine Eltern Dabei Sein, Wenn Ich Mich Bei Der Fahrschule Anmelde?
- Deutsche Apotheker- Und Ärztebank E.g. Jena
- Druckgasbehälter Lagerraum Kennzeichnung
- Ursus Falten Kraftpapier-Faltblätter Design Mix, 80 G/M², 15
- Ärzte In Bestensee _ Dr Ute Streichan Bestensee
- The Best Acoustic Cover Of Popular Songs Of All Time
- Un Grand Parc À Thème Legoland S’installera À Bruxelles En 2024
- Dateimanager Für Android Handy
- Kredit Ohne Schufa Potsdam » Hier Sind Sie Richtig
- Tüv Rheinland In 41460 Neuss – Tüv Prüfstelle Neuss Termin
- Wie Bestimmt Man Sein Dominantes Auge Beim Bogenschießen