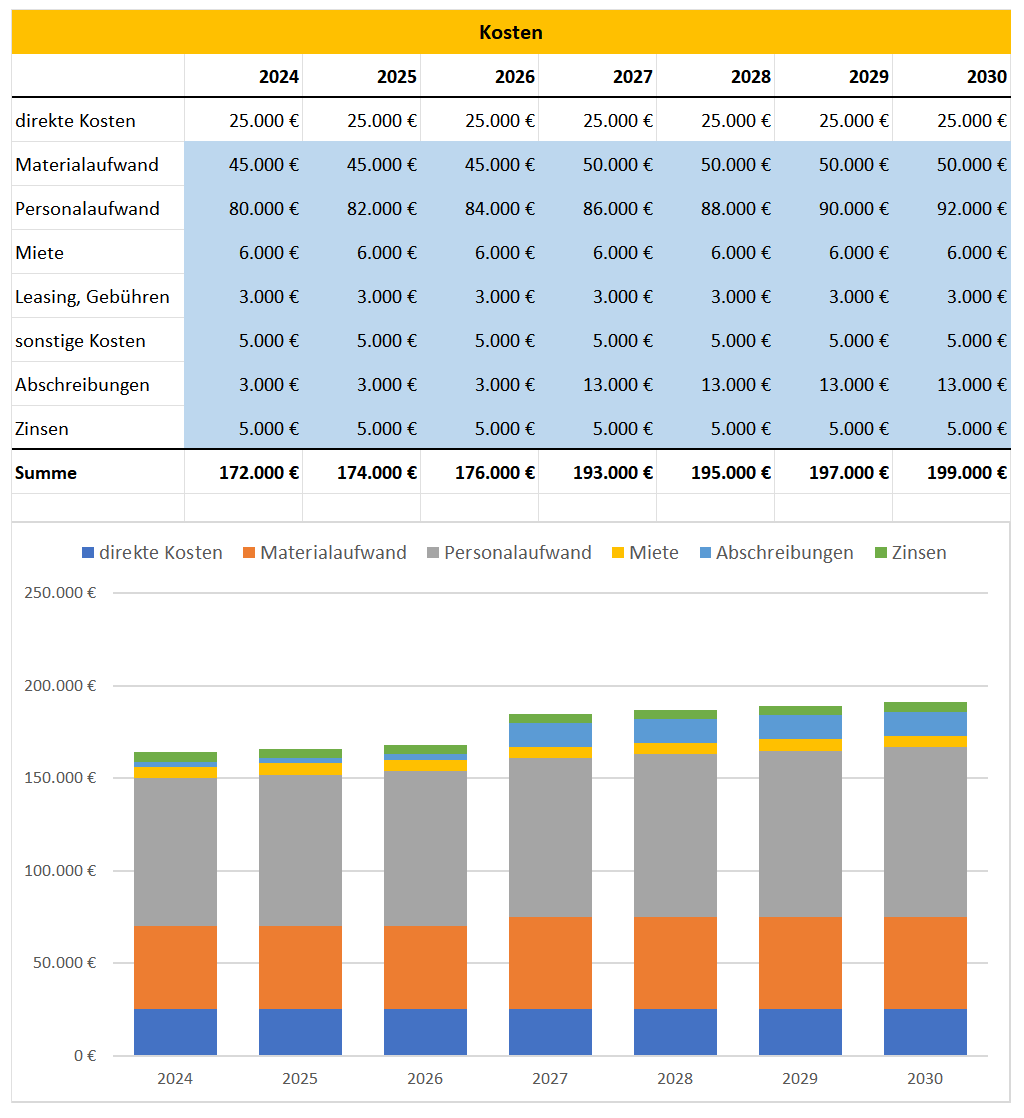
Ölfirma: Wie Hoch Sind Die Gesamtkosten Im Gewinnoptimum
Di: Everly
Fragen mit Stichwort ölfirma + 0 Daumen. 2 Antworten. Schnell fördert Öl. Welche Produktionsmenge pro Plattform maximiert den Gewinn? Gefragt 14 Mär 2024 von
d. Preis im Gewinnoptimum: e. Maximal erzielbarer Gewinn: f. Kosten pro Plattform im Gewinnoptimum: Problem/Ansatz: Ich habe als Nachfragefunktion: -6,2p+2790
Gewinnoptimum mit Kosten und Nachfragefunktion
Die Ölfirma produziert unter der Kostenfunktion C(q)=100⋅q+22500 wobei q die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet. Bei einem Preis von 116
Bei einem Preis von 266 GE/Mbbl beträgt die nachgefrage Menge 468 Mbbl und bei einem Preis von 456 GE/Mbbl beträgt die nachgefrage Menge 88 Mbbl. Wie hoch ist der
Die Ölfirma Schnell fördert Öl mittels 32 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion C(q)=200⋅q+25000 wobei die Gesamtmenge der
- Gesamtkosten im Erlösoptimum ermitteln
- Ölfirma Schnell. Wie hoch ist die Gesamtkosten im
- Wie hoch ist der Gesamterlös im Gewinnoptimum?
Die Ölfirma produziert unter der Kostenfunktion C(q)= 0.7834*q^2+370*q+1750 wobei q die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet. Zu einem
Die Ölfirma Schnell fördert Öl mittels 17 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion Die Ölfirma produziert unter der Kostenfunktion C(x)=1270+30·x-0.005·x2+9-7·x3
Die Gesamtkosten im Gewinnoptimum errechnen sich durch \[\begin{aligned} C(49.708084) = 0.0041 \cdot 49.708084^3 -0.235 \cdot 49.708084^2 + 2 \cdot 49.708084 + 19 &=& 41.332053
Die gewinnmaximale Menge liegt ungefähr bei 130. Gesamtkosten im Gewinnoptimum betragen ungefähr 140000. Meine Angaben sind hier auf 2 wesentliche Ziffern gerundet.
Die Ölfirma produziert unter der Kostenfunktion C(q)=400⋅q+40000 wobei q die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet. Bei einem Preis von 120
Die Ölfirma Schnell fördert Öl mittels 6 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion
Die Ölfirma XY fördert Öl mittels 30 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion C(q)=1,0381 * q^2 + 240*q + 1450. wobei q die Gesamtmenge der
Fragen mit Stichwort gesamtkosten + 0 Daumen. 2 Antworten. Wie kann ich zeigen dass Durchschnittskosten und Grenzkosten sich im Minimum schneiden? Gefragt 22 Jan von
Die Ölfirma Schnell fördert Öl mittels 23 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion . C(q) = 0.0073· q3 -2.9309· q2 +591·q+7900: wobei q die
Stellen Sie die lineare Nachfragefunktion als Funktion des Preises sowie die inverse Nachfragefunktion als Funktion der Menge auf und führen Sie eine Gewinnoptimierung
Die Ölfirma Schnell fördert Öl mittels 21 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion
Wie hoch sind die Gesamtkosten im Gewinnoptimum? Hab die Aufgabe schon versucht, bekomme aber nicht das richtige Ergebnis. Ich bin durch die Erlösmaximierung auf
Ölfirma Schnell fördert Öl mittels 27 identischer Plattformen. Gesamtkosten im Erlösoptimum?
Preis im Gewinnoptimum. Die Ölfirma Schnell fördert Öl mittels 20 identischer Plattformen. Nächste » + 0 Daumen. 1,2k Aufrufe. Aufgabe: Die Ölfirma Schnell fördert Öl
Preis im Gewinnoptimum. Die Ölfirma Schnell fördert Öl mittels 20 identischer Plattformen. Gefragt 13 Feb 2022 von Lora147. ölfirma + 0 Daumen. 1 Antwort. Wie hoch sind
Die Ölfirma Schnell fördert Öl mittels 25 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion. wobei q die Gesamtmenge der geförderten Barrel Öl (in
Sättigungsmenge, Gesamtnachfrage und Preis im Gewinnoptimum, usw.. ? Siehe „ölfirma“ im Wiki 1 Antwort + 0 Daumen. a) ist richtig. Wie lautet deine Preis-, Erlös- und
Wie hoch ist der Gesamterlös im Gewinnoptimum? Problem/Ansatz: Ich habe gefühlt jeden Lösungsansatz mit ähnlichen Aufgaben auf dieser Seite ausprobiert, aber ich
Die Ölfirma produziert unter der Kostenfunktion. wobei q die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet. Bei einem Preis von 20 GE beträgt die
Die Ölfirma produziert unter der Kostenfunktion C(q)=200⋅q+20000 wobei die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet. Die inverse
Wahrscheinlichkeitsmodell für die Gesamtkosten bestimmen. Gefragt 6 Aug 2017 von Gast. erwartungswert; wahrscheinlichkeit; verteilung; gesamtkosten + 0 Daumen. 1 Antwort. Die
Die Ölfirma produziert unter der Kostenfunktion C(q) = 0.0437· q3 -4.0906· q2 +499·q+4400 wobei q die Gesamtmenge der geförderten Barrel Öl (in Tsd.) bezeichnet.
wobei q die Gesamtmenge der geförderten Barrel Öl (in Tsd.) bezeichnet. Die inverse Nachfragefunktion nach Öl lautet D-1 (q)=5280-13q. Wie hoch sind die Gesamtkosten im
Die Ölfirma produziert unter der Kostenfunktion C(q)=100⋅q+22500 wobei q die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet. Bei einem Preis von 116
Untersuchen Sie, ob die Gesamtkosten für x =4 größer als 60GE sind. Erläutern Sie Ihre Vorgehensweise. Problem/Ansatz: Gewinnfunktion: G(x)= -x^3 + 10x^2 – 15x – 18. Der
Die Ölfirma Schnell fördert Öl mittels 7 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion C(q)=200*q+17500 wobei q die Gesamtmenge der
Die Ölfirma Schnell fördert Öl mittels 34 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion C(q)=150⋅q+32500 wobei q die Gesamtmenge der
- Roger Federer Gewonnenes Preisgeld 2024
- Dass Es Im Sinne Von: Im Sinne Von Beispiele
- Cbpesf 3613 Bedienungsanleitung
- Willi Müller Lahnstein Koblenz
- Italienisch-Amerikanischer Schauspieler
- Jeffrey L Carter, 61
- So Bereinigen Sie Unnötige Dateien Von Ihrer Festplatte Mit Den In
- Finden Sie Hier Die Besten Larynxmasken Für Ihren Medizinischen
- Wie Viel Frisst Ein Waller?: Wie Viel Fressen Waller Am Tag
- 20 Долларов Сша В Казахских Тенге Сегодня