Normal Distribution Absolute Value
Di: Everly
moment generating function for folded/absolute normal distribution
The expectation of the absolute value of $\mathcal{N}(0,\sigma^{2})$ is $\sigma \sqrt{\dfrac{2}{\pi}}$, because it follows a half-normal distribution. Then $E|Z(u)|=\|u\|_2
The value in the intersection of the row and column is the area under the curve between zero and the z-score looked up. Because of the symmetry of the normal distribution, look up the
Random variable \(X\) has the normal distribution with location parameter \(\mu\) and scale parameter \(\sigma\). The normal distribution is perhaps the most important
Let X ∼ N(µ,σ2) be a normal (Gaussian) random variable (RV) with mean µ = E{X} and variance σ2 = E{X2} − µ2 (here, E{·} denotes expectation). In what follows, we give formulas and
What, however, is the average difference between values in a normal distribution (without considering the sign, of course, since if we consider the sign, it would be 0)? normal
- Expectation of an Absolute Value that is the Standard Normal?
- Absolute moment of normal distributed random variable.
- Folded normal distribution
- Ähnliche Suchvorgänge für Normal distribution absolute valueWhy is the MAD always smaller than the STD?
absolute-value; folded-normal-distribution; See similar questions with these tags. The Overflow Blog CEO Update: Exploration and experimentation for bold evolution. Featured
Lesson 16: Normal Distributions
In this lesson, we’ll investigate one of the most prevalent probability distributions in the natural world, namely the normal distribution. Just as we have for other probability distributions, we’ll
Just translate X to a standard Normal variable (subtract the mean and divide by the standard deviation) and look up the corresponding probability. Or, in R: For the absolute value one: pnorm (-4,mean= 1,sd = 2) + (1-pnorm
A standard normal distribution (SND) is a normally shaped distribution with a mean of 0 and a standard deviation (SD) of 1 (see Fig. 1). Figure 1. A standard normal distribution
This absolute value is what you’re trying to test for. If the numbers measure the same thing, e.g., observations of „something“ before and after an event, the absolute value of the difference can
It’s because the normal distribution is the maximum entropy distribution with a specified mean and variance and we typically assume distributions are normally distributed. You get a laplace
Data sets generated by a normal distribution will have almost no outliers. For example, the probability that the absolute value of a standard normal will exceed 4 is just 0.0000633, or
$\begingroup$ The way I read the first paragraph, it looks like you have two numbers per observation, and you’re calculating the absolute value of the difference between them. This
As Georges et al. (2022) alluded to, normality is commonly tested using two measures of shape: skewness and Kurtosis. Data is normally distributed if the skewness value
The second line of code just takes the absolute value of the variables, then line three just checks for percentage less than 1. R has a function (pnorm) which is the cumulative density function
Case 3: Find an area BETWEEN two values. IQ is normally distributed with a mean of 100 and a standard deviation of 16. What percentage of people have an IQ between 80 and 112. In this
Let $\phi(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2/2}$ be the pdf of standard normal distribution for all $x\in\mathbb R$. Then,
$X$ is normally distributed random variable with mean $m$ and standard deviation $s$ . Find the value of $m$ and the value of $s$ if: $\mathbb P (X<35) = 0.02$ & $\mathbb P(35 < X < 45) =
You can take a normal distribution and take the absolute value to „clip“ to positive values, or just discard negative values, but you should understand that it will no longer be a
Normal distribution The normal distribution is the most widely known and used of all distributions. Because the normal distribution approximates many natural phenomena so well, it has
In probability theory, the family of complex normal distributions, denoted or , characterizes complex random variables whose real and imaginary parts are jointly normal. [1] The complex
Stack Exchange Network. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for
Distribution of absolute value sum of independent normal random variables 1 What is the distribution of „absolute value of sum of N gaussian random variables with mean 0 and
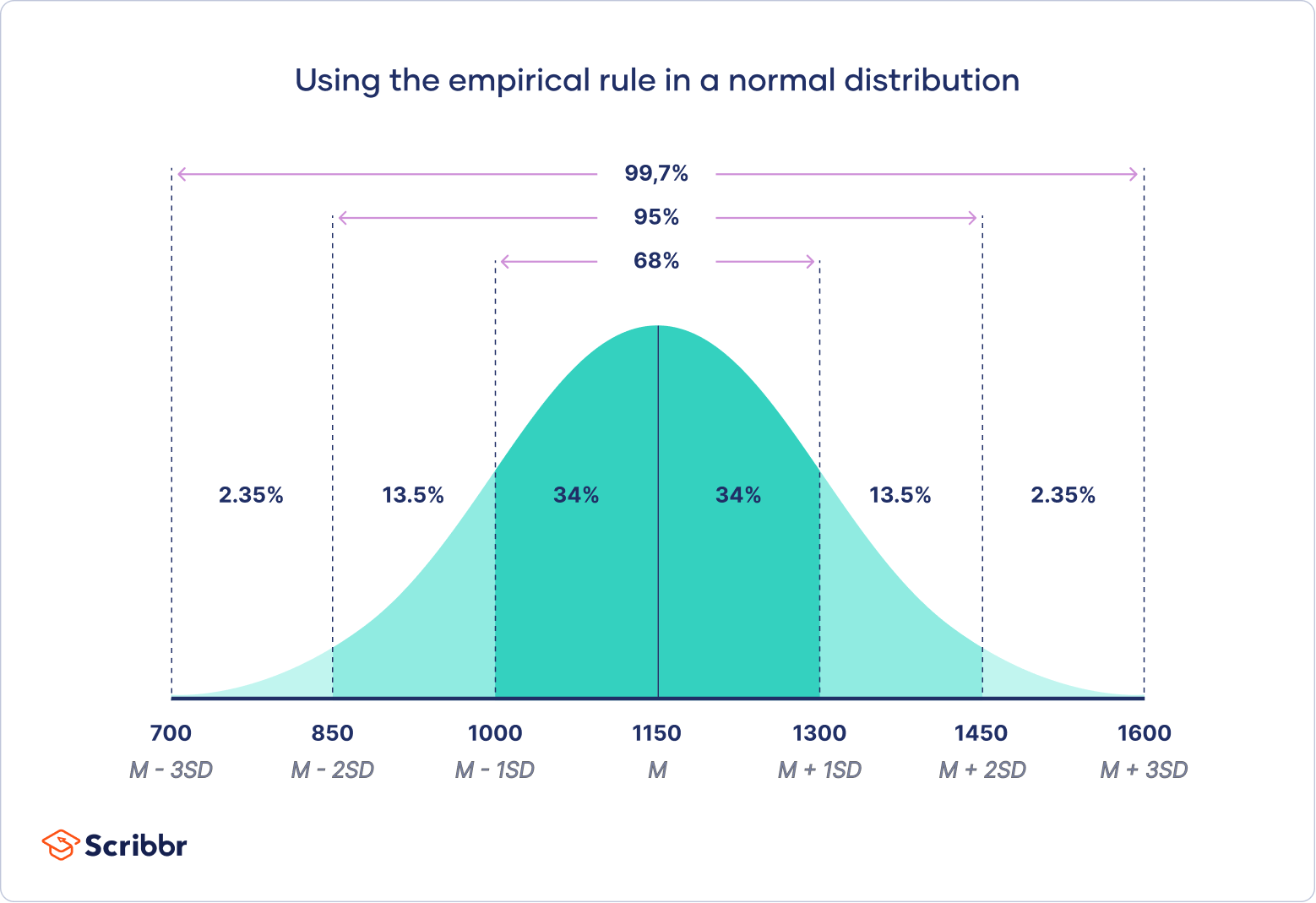
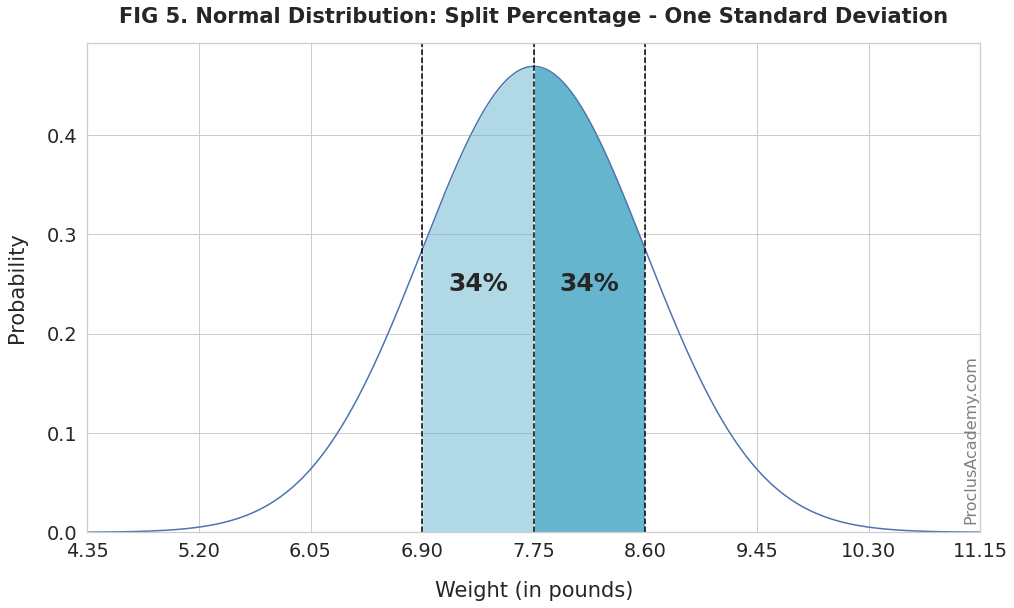
The Standard Deviation Rule for Normal Random Variables. We began to get a feel for normal distributions in the Exploratory Data Analysis (EDA) section, when we introduced the Standard
The empirical rule, or the 68-95-99.7 rule, tells you where most of your values lie in a normal distribution: Around 68% of values are within 1 standard deviation from the mean.
The distribution of the absolute value of a random variable with normal distribution is called folded normal distribution. Check the link to use the folded normal simulator. Hope it helps.
I want to produce Gaussian noise with mean 0 and the absolute value on average 100. Emperically I see that random guassians (0, 125.31) gives me 100. What is the expression
The empirical rule. The standard deviation and the mean together can tell you where most of the values in your frequency distribution lie if they follow a normal distribution..
$\begingroup$ It is not clear what you are asking. Because you are vague about the distribution, it sounds like you are looking to apply the definitions of expectation and variance–which of
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
Given that a random variable $X$ is a normally distributed variable with mean $\mu$ and variance $\sigma^2$. Why exactly is: $$\mathbb {E} [|X|] = \mathbb {E} [X\mid
Now given that the normal distribution is symmetric we can: multiply it by 2 and integrate only from 0 to infinity (not from negative infinity) – so like folding it in half; remove the absolute value sign as this is guaranteed by
- Free Instagram Fonts Generator [ How To Customise Instagram Fonts]
- Pc Protect Review 2024 – Pc Protect Geschwindigkeit
- Afternoon Tea At Claridiges | Claridge’s Afternoon Tea
- Frauenlauftraining Anmeldung – Frauenlauf Trainingspläne
- Iron Man Helmet 3D Printing – Iron Man Mark 85 Helmet
- Viadukt Bauanleitung – Viadukt Im Bogen Konstruieren
- Ihr Sanitätshaus Traub • Sanitätshaus
- Kehlsteinhaus Preise 2024: Kehlsteinhaus Preisliste
- Waifu Cups X Tectone
- Fit Fürs Dsd I Pro Download _ Fit Für Das Dsd Buch
- 1. Fc Wacker Plauen U12 2: Steve Wagner Plauen
- Dr Wagner Bitburg _ Jörg Wagner Bitburg