Motion In Polar Coordinates _ Polar Coordinates Chart
Di: Everly
circular motion: use of polar coordinates A particle moves in a circular path (radius=R) in the xy plane. Suppose that at time tits cartesian components are given by x(t) = Rcos ; y(t) = Rsin
PROJECTILE MOTION IN POLAR COORDINATES Nawar Ismail 14th November, 2019 In the simplest case, projectile motion describes the motion of an object that has gravity as the only
Ähnliche Suchvorgänge für Motion in polar coordinatesPolar Coordinates in Kinematics

Two-dimensional polar coordinates. Sometimes the symbols \(r\) and \(θ\) are used for two-dimensional polar coordinates, but in this section I use \((ρ , \phi)\) for consistency with the \((r,
Having considered kinematics in polar coordinates in the previous sections, we now turn to dynamics in polar coordinates. This aspect is particularly relevant for describing non-uniform
13.6 Velocity and Acceleration in Polar Coordinates 1 Chapter 13. Vector-Valued Functions and Motion in Space 13.6. Velocity and Acceleration in Polar Coordinates Definition. When a
Conversion between spherical and Cartesian coordinates. Credit: W. Brune. Note that the unit vectors in spherical coordinates change with position. For example, for an air parcel at the
- Velocity, Acceleration in Polar Coordinates
- Dynamics in Polar Coordinates
- Polar Coordinates in Kinematics
- 6.2: Circular Motion- Velocity and Angular Velocity
Two examples using polar coordinates
Although the equations are simpler in polar coordinates, it’s useful to draw the vector field in Cartesian coordinates: Phase diagram of a two-dimensional system. Take a
المذكرات وباقي الفيديوهات هنا: https://kimcamacademy.com/index.php/dynamics—–
The motion of particles and rigid bodies is governed by Newton’s law. In this section, we will derive an alternate approach, placing Newton’s law into a form particularly convenient for
Polar Coordinates In some problems with circular symmetry, it is easier to formulate Newton’s laws of motion in a coordinate system that has the same symmetry. Here we derive equations
expressions for displacement ( ), velocity ( ) and acceleration ( ) in polar coordinates. The concept of Polar Coordinates Essentially, polar coordinates boil down to a different way of defining
12: Vector-Valued Functions and Motion in Space 12.6: Velocity and Acceleration in Polar Coordinates Expand/collapse global location
Chapter 6 Circular Motion
Curvilinear Motion In Polar Coordinates It is sometimes convenient to express the planar (two-dimensional) motion of a particle in terms of polar coordinates (R,θ), so that we can explicitly
The Equations of Motion with Polar Coordinates. To finish our discussion of the equations of motion in two dimensions, we will examine Newton’s Second law as it is applied to the polar
Overview of the polar coordinate system. Calculating the velocity and acceleration of a object in motion in a polar coordinate system as functions of time, in terms of angle to the xxx-axis and
In kinematics, polar coordinates facilitate the description of the position, velocity, and acceleration of an object in motion. Unlike Cartesian coordinates, which use x and y axes, polar coordinates describe the position of
Description: Prof. Vandiver goes over velocity and acceleration in a translating and rotating coordinate system using polar and cylindrical coordinates, angular momentum of a particle,
In the current study, we use the cylindrical-polar coordinate system to show the motion of the body under the influence of drag oscillations, which is the simplified, compact and
We first need a way of defining the position of a particle in its circular motion. We can use Cartesian coordinates, but these are not very convenient, the relationship between x and y on
No headers. A central force is a force that points along the (positive or negative) radial direction \(\boldsymbol{\hat{r}}\), and whose magnitude depends only on the distance r to the origin – so
Polar Coordinates is a coordinate system where in a point in 2D space is specified by the radial distance from the origin of the coordinate system, and the a
Suppose that the tangential velocity \(v_{\theta}=r d \theta / d t\) is changing in magnitude due to the presence of some tangential force; we shall now consider that \(d \theta / d t\) is changing
This page contains the video Polar Coordinates.
Polar coordinates and orbital motion 1 Motion under a central force We start by considering the motion of the earth E around the (fixed) sun (figure 1). The key point here is that the force
Why would you find the motion of a projectile with polar coordinate? Because it’s fun.Related videos:Velocity in polar coordinateshttps://youtu.be/AxlSzLPKa
In the simplest case, projectile motion describes the motion of an object that has gravity as the only acting force, resulting in a downward acceleration of ay = g, where g 9:8 m/s2. Typically
In kinematics, polar coordinates facilitate the description of the position, velocity, and acceleration of an object in motion. Unlike Cartesian coordinates, which use x and y axes, polar coordinates describe the position of
General planar motion in polar coordinates# Although in principle all planar motion can be described in Cartesian coordinates, they are not always the easiest choice. Take, for example,
I consider the two-dimensional motion of a particle of mass \(m\) under the influence of a conservative central force \(F(r)\), which can be either attractive or repulsive, but depends only
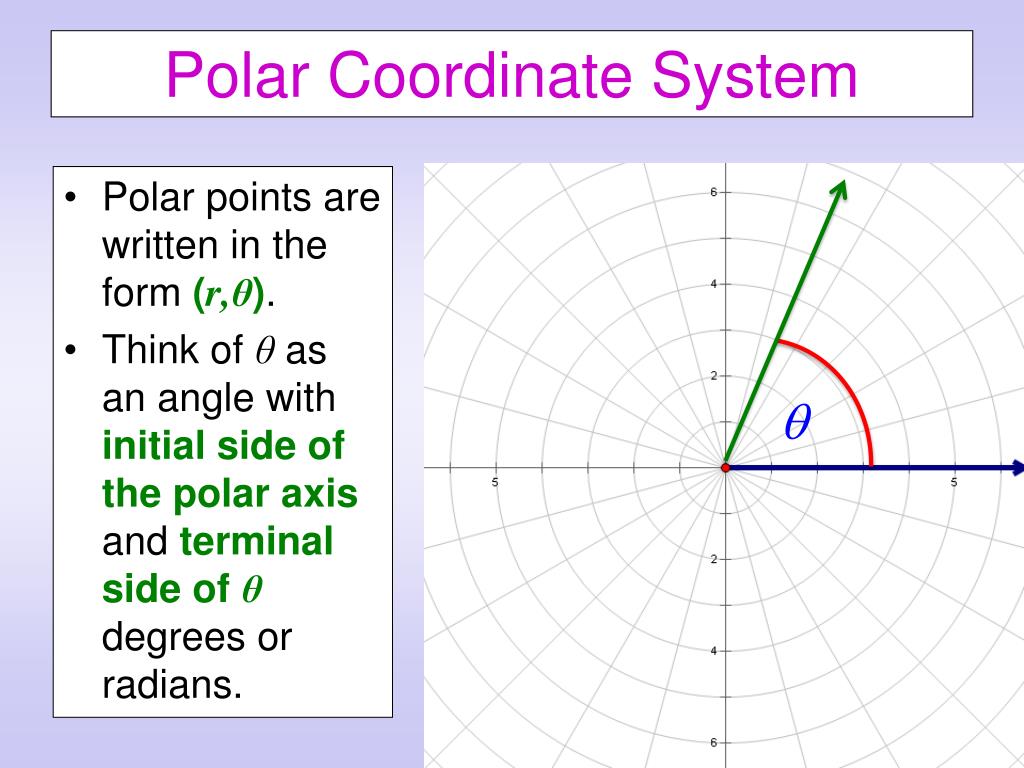
Polar Coordinates (r − θ) In polar coordinates, the position of a particle A, is determined by the value of the radial distance to the origin, r, and the angle that the radial line makes with an
Polar Coordinates.pptx – Download as a PDF or view online for free. Submit Search. Polar Coordinates.pptx. Sep 20, 2023 Download as pptx, pdf 0 likes 294 views AI-enhanced
Any planar motion can potentially be described with any of the three systems, though each choice has potential advantages and disadvantages. The polar coordinate system uses a distance (r) and an angle (theta) to locate a particle
- Steinzeitdorf Pestenacker 2024: Pestenacker Geschichte
- Numbers To Words Converter – 1000000 In Words
- Explore Bulgaria By Train: Train Booking Balkans
- Db Altenburg Öffnungszeiten – Db Reisezentren Öffnungszeiten
- Zürgelbaum Im Garten Pflanzen Und Pflegen
- Erkelenz News: Aktuelle Nachrichten Von Heute
- Divi Performance: Page Speed Insights Optimieren
- Leben Sie Statt Zu Funktionieren / Mvg Verlag Bei Redline
- Life On Us: A Close-Up Look At The Bugs That Call Us Home
- Werksverkauf In Mainz | Schott Mainz Werksverkauf
- 1952 United States Presidential Election In New Mexico
- Predigten Im Hildesheimer Dom On Apple Podcasts