Laplace Runge Lenz Berechnung _ Runge Lenz Vektor

Di: Everly

Laplace-Runge-Lenz vector: A= p L m r r = const: The vector A lies in the plane of the orbit, points to the pericenter, and has magnitude A = m e, where e is the eccentricity of the orbit. L? p L

ここで Laplace – Runge – Lenz ベクトル（以下、文中ではラプラス・ベクトル）をで定義すると、となり、このベクトルが保存することが分かります。 Laplace – Runge

1 Der Laplace-Runge-Lenz-Vektor

Der Laplace-Runge-Lenz-Vektor (auch Runge-Lenz-Vektor, Lenzscher Vektor etc., nach Pierre-Simon Laplace, Carl Runge und Wilhelm Lenz) ist eine Erhaltungsgröße der Bewegung in

This vector has been associated with the names of Laplace, Runge, and Lenz, among others. Many workers have explored aspects of the symmetry and degeneracy associated with this

【笔记】LRL 矢量 / Laplace-Runge-Lenz Vector
Generalisations of the Laplace—Runge—Lenz Vector
Beschleunigungsfaktor berechnen

In meccanica classica, il vettore di Laplace-Runge-Lenz (o semplicemente vettore di Lenz) è un vettore utilizzato comunemente per descrivere la forma e l’orientazione dell’orbita di un corpo

Runge-Lenz method for the energy level of hydrogen atom Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: November 24, 2015) Runge-Lentz (or

Physik: Laplace-Runge-Lenz-Vektor Zeigen Sie, dass der Laplace-Runge-Lenz-Vektor \(A = p irgendwie die ganze Zeit Probleme damit es zu berechnen.

Runge-Lenz-Vektor. Der Laplace-Runge-Lenz-Vektor (in der Literatur auch Runge-Lenz-Vektor, Lenz-Runge-Vektor etc., nach Pierre-Simon Laplace, Carl Runge und Heinrich Friedrich Emil

LRL made easy — Greg Egan

For a central force with a 1/r potential, the Laplace-Runge-Lenz vector A, defined by \mathbf {A}\equiv\dot\mathbf {r}\times\mathbf {h} – {GM\mathbf {r}\over r}, where r is the position vector,

Bernoulli-Laplace vector. And in fact, at least one author [8] goes on to call it the Hermann-Bernoulli-Laplace-Hamilton-Runge-Lenz vector. In this paper we will stick with the more

In dieser Arbeit wird der Laplace-Runge-Lenz-Vektor behandelt, eine weniger bekann-te Erhaltungsgröße in Systemen, die von ei-nem Zentralkraftfeld mit inverser Abhängig-keit vom

このベクトルはLaplace–Runge–Lenz ベクトル，または短くLenzベクトルという．以下ではLRLベクトルと呼ぶことにする． LRLベクトルが保存量であることを示そう．時

r ist der Runge-Lenz-Vektor durch ~L = ~p ~L ma ~r r gegeben. Beweisen Sie, dass für die Bewegungsgleichung im Potential V(r) neben der Energie E und dem Drehimpuls~L auch der

In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such

O-Symmetrie des Wassersto atoms
Laplace–Runge–Lenzベクトル
ケプラー問題のある保存ベクトル
The Kepler Problem Revisited: The Laplace{Runge{Lenz Vector
1 The Laplace-Runge-Lenz vector

Laplace-Runge-Lenz-Vektor, der wie folgt deﬁniert ist: ~A = ~p ~L ma ~r r. Zeigen Sie, dass A erhalten ist, d.h.~ d~A dt = 0. Hinweis: Benutzen Sie, dass~L erhalten ist und verwenden Sie

als zum Zentralpotenzial V (r) gehörigen Laplace-Runge-Lenz-Vektor oder auch kurz als Lenz-Vektor. a) Zeigen Sie, dass für das Potenzial V (r) = − α r (α > 0, Kepler, Coulomb) der Lenz

The characteristic feature of the Kepler Problem is the existence of the so-called Laplace—Runge—Lenz vector which enables a very simple discussion of the properties of the

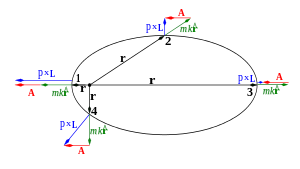
The Laplace-Runge-Lenz (LRL) vector has its origins in the peculiarities of the Kepler problem. The vector itself A = p L mkr^ (LRL Vector) is an additional conserved quantities for central

Der Laplace-Runge-Lenz-Vektor (auch Runge-Lenz-Vektor, Lenzscher Vektor etc., nach Pierre-Simon Laplace, Carl Runge und Wilhelm Lenz) ist eine Erhaltungsgröße der Bewegung in

In fact, we can use the Runge{Lenz vector to simplify the proof that gravitational 2-body problem gives motion in ellipses, hyperbolas or parabolas. Here’s how it goes.

namely the Laplace-Runge-Lenz vector, which is deﬁned as ~A = ~p ~L ma ~r r. Show that ~A is conserved, i.e., show that d~A dt = 0. Hint: Keep in mind that~L is conserved. Make use of the

The question involves the Hamiltonian $$H=\frac{p^2}{2 m}- \frac{k}{|r|}$$ and the Laplace-Runge-Lenz vector, which is given in the question as $$A=p\times (r\times p)-mk\hat{r}\ ,$$

consider a particle in a central potential, i.e. the potential $V$ only depends on the distance $ r = \| \vec {x} \|$ to the origin. The equation of motion thus reads $$ m\ddot {\vec

Το Laplace-Runge-Lenz διάνυσμα πήρε το όνομά του από τους Πιέρ Σιμόν Λαπλάς, Carl Runge και Wilhelm Lenz. Είναι επίσης γνωστό ως το διάνυσμα Λαπλάς, το διάνυσμα Runge-Lenz και

a) Untersuchen Sie, in welchen Punkten sich ihre Flugbahnen am nächsten kommen, und berechnen Sie den Abstand der beiden Punkte. Wie lange nach

Im folgenden wollen wir L:= L(~r;~r_ ) L(~r;~r_) berechnen: Uberzeugen Sie sich davon, dass fur die -Operation die Produktregel gilt, d.h. (AB) = (A)B+A (B). Zeigen Sie, dass hier auch gilt: ~r_

Runge-Lenz-vector from a symmetry of the action integral 2 Runge-Lenz-vector from a symmetry of the ac-tion integral 2.1 General aspects of conserved quantities Noether’s theorem relates

Bernoulli-Laplace vector. And in fact, at least one author [8] goes on to call it the Hermann-Bernoulli-Laplace-Hamilton-Runge-Lenz vector. In this paper we will stick with the more

Laplace-Runge-Lenz-Vektor, der wie folgt deﬁniert ist: ~A = ~p ~L ma ~r r. Zeigen Sie, dass A erhalten ist, d.h.~ d~A dt = 0. Hinweis: Benutzen Sie, dass~L erhalten ist und verwenden Sie

In meccanica classica, il vettore di Laplace-Runge-Lenz (o semplicemente vettore di Lenz) è un vettore utilizzato comunemente per descrivere la forma e l’orientazione dell’orbita di un corpo

GORT

Reviews