Full Explanation Of Non-Homogeneous Differential Equation

Di: Everly

A linear differential equation is homogeneous if it is a homogeneous linear equation in the unknown function and its derivatives. It follows that, if φ(x) is a solution, so is cφ(x), for any

8.1: Basics of Differential Equations

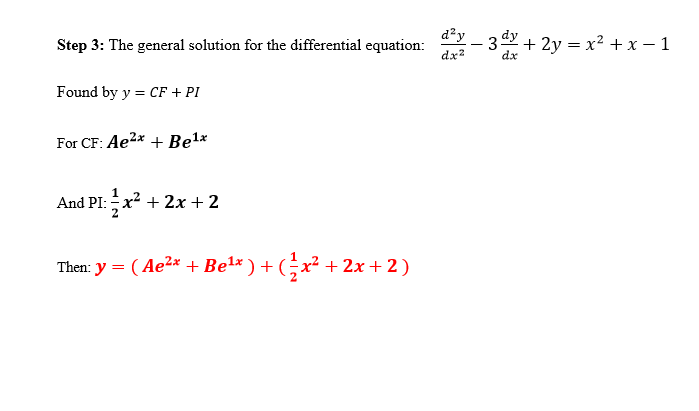
Non-Homogeneous Second Order Differential Equations - MATH MINDS ACADEMY

Thus, YP is a solution to the non-homogeneous differential equation. The entire solution can be checked as follows. > simp1ify(subs(y(x) = rhs(so11), deq1)); Consider the following non

This set of Ordinary Differential Equations Multiple Choice Questions & Answers (MCQs) focuses on “Separable and Homogeneous Equations”. 1.

For simplicity, we restrict ourselves to second order constant coefficient equations, but the method works for higher order equations just as well (the computations

In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous differential equation. We work a wide variety of

In this section we will discuss the basics of solving nonhomogeneous differential equations. We define the complimentary and particular solution and give the form of the

Diﬀerential Equations HOMOGENEOUS FUNCTIONS
Nonhomogeneous Equations in General
Introduction to Partial Differential Equations

6.9 Nonhomogeneous Linear Systems

to a homogeneous second order differential equation: y“ p(x)y‘ q(x)y 0 2. Find the particular solution y p of the non -homogeneous equation, using one of the methods below. 3. The

Homogeneous differential equation is a differential equation of the form dy/dx = f(x, y), such that the function f(x, y) is a homogeneous function of the form f(λx, λy) = λnf(x, y), for any non zero

Diﬀerential Equations HOMOGENEOUS FUNCTIONS Graham S McDonald A Tutorial Module for learning to solve diﬀerential equations that involve homogeneous functions Table of

the nonhomogeneous differential equation can be written as ?( ) ( )= ( ). The general solution ( ) of the nonhomogeneous differential equation is q sum of the general solution 0( ) of the

To solve ordinary differential equations (ODEs) use the Symbolab calculator. It can solve ordinary linear first order differential equations, linear differential equations with constant coefficients,

In this section we will work quick examples illustrating the use of undetermined coefficients and variation of parameters to solve nonhomogeneous systems of differential

Non-homogeneous Equation; Method of Undetermined
Homogeneous System of Linear Equations
The Method of Variation of Parameters
8.1: Basics of Differential Equations
CHAPTER Non-homogeneous Linear Differential Equations

Systems of Differential Equations. In this section, we study the nonhomogeneous linear system. y ′ = A y + f (t) (6.9.1) where matrix A is an n × n matrix function and f is an n -vector forcing

Lecture 22 : NonHomogeneous Linear Equations (Section 17.2) where yp(x) is a particular solution of ay00 + by0 + cy = G(x) and yc(x) is the general solution of the complementary

8.2 Typical form of second-order homogeneous differential equations (p.243) ( ) 0 2 2 bu x dx du x a d u x (8.1) where a and b are constants The solution of Equation (8.1) u(x) may be obtained

1 Many texts refer to the general solution of the corresponding homogeneous differential equation as “the comple-mentary solution” and denote it by yc instead of y h. We are using y to help

If a homogeneous system of linear equations has more variables than equations, then it has a nontrivial solution (in fact, infinitely many). Note that the converse of Theorem

DIFFERENTIAL EQUATIONS - PART 5(NON HOMOGENEOUS EQUATIONS)(SUPER TRICKS ...

Section 7.2 : Homogeneous Differential Equations. As with 2 nd order differential equations we can’t solve a nonhomogeneous differential equation unless we can first solve the

try to solve nonhomogeneous equations P(D)y = F(x): Recall that the solutions to a nonhomogeneous equation are of the form y(x) = y c(x)+y p(x); where y c is the general

The method of undetermined coefficients is a use full technique determining a particular solution to a differential equation with linear constant-Coefficient. Theorem The form

The final quantity in the parenthesis is nothing more than the complementary solution with c 1 = -c and \(c\) 2 = k and we know that if we plug this into the differential

where yh(t) is a general solution to the homogeneous equation Ly = 0 and yp(t) is a particular (any) solution to (1). In the last lecture we saw how to guess yp(t) by looking at the expression

Write the general solution to a nonhomogeneous differential equation. Solve a nonhomogeneous differential equation by the method of undetermined coefficients. Solve a nonhomogeneous

NONHOMOGENEOUS LINEAR EQUATIONS 5 We summarize the method of undetermined coefﬁcients as follows: 1. If , where is a polynomial of degree , then try , where is an th-degree

Note that a solution to a differential equation is not necessarily unique, primarily because the derivative of a constant is zero. For example, \(y=x^2+4\) is also a solution to the

An ordinary differential equation is a differential equation in which a dependent variable (say ‘y’) is a function of only one independent variable (say ‘x’). A partial differential equation is one in

The general solution, y GNH, of a linear nonhomogeneous equation a y ″ + b y ′ + c y = f (t) is obtained by finding a particular solution, y PNH, of the nonhomogeneous equation and adding

This article covers the fundamentals needed to identify non-homogeneous differential equations and two important methods that will help you find their solutions. What Is a Non Homogeneous

Example 1: Solve d 2 ydx 2 − 3 dydx + 2y = e 3x. 1. Find the general solution of d 2 ydx 2 − 3 dydx + 2y = 0. The characteristic equation is: r 2 − 3r + 2 = 0. Factor: (r − 1)(r − 2) = 0. r = 1 or 2. So

Ordinary Differential Equation: In Calculus, the Ordinary Differential Equation (ODE) is defined as an equation which has only one independent variable and it can have one or more derivatives

A non-homogeneous equation of constant coefficients is an equation of the form d n y d x n + c 1 d n − 1 y d x n − 1 + + c n y = f ( x ) {\displaystyle {\frac

Write the general solution to a nonhomogeneous differential equation. Solve a nonhomogeneous differential equation by the method of undetermined coefficients. Solve a nonhomogeneous

GORT

Reviews