Examples Of Lagrange Interpolation
Di: Everly
• Note that Lagrange interpolation is a special case of Hermite interpolation ( , i.e. no derivatives are matched). • It is also possible to set up specialized Hermite interpolation functions which do
There are different methods for interpolation for example: Newtons Forward Interpolation, Netwtons Backward Interpolation, Newtons General Interpolation with divided difference,
LECTURE 3 LAGRANGE INTERPOLATION
We can use interpolation techniques to find an intermediate data point say at x = 3. Advantages of Lagrange Interpolation: This formula is used to find the value of the function
The popular usage of Lagrange Polynomials includes the Newton-Cotes method to find the numerical integration or secret scheme in cryptography. It is used to check the
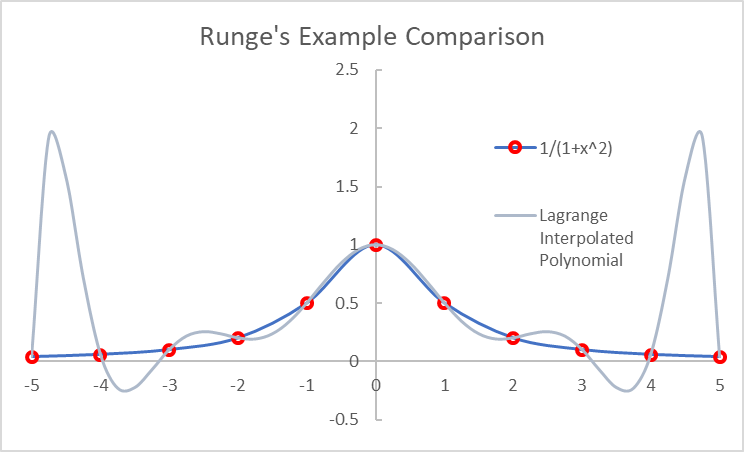
Polynomials are usually not written in their Lagrange form. They are usually written in theirpower form; e.g., the previous Lagrange polynomial can be written as x3 2x 5: Of course, a
- Polynomial interpolation: Lagrange interpolation
- An Overview of Lagrange Interpolation Formula
- Interpolation and Lagrange polynomial
- LAGRANGE INTERPOLATION Introduction n
LAGRANGE INTERPOLATION DARYL DEFORD 1. Introduction Polynomial interpolation is a method for solving the following problem: Given a set of n of data points with distinct
2 Polynomial interpolation (Lagrange) One approach to approximation is called interpolation. Suppose we have the data ‘nodes’ x 0; ;x n; values f j = f(x j); j= 0;1; ;n: (1) An interpolant for
We discuss Lagrange’s formula and error bounds in two lectures. The interpolating polynomial is easily described once the form of Lk is known, by the following theorem. k = 0; 1; : : : ; n. This
LAGRANGE INTERPOLATION Introduction n
If the values of x are at equidistant or not at equidistant, we use Lagrange’s interpolation formula. Let y = f( x) be a function such that f ( x) takes the values y 0 , y 1 , y 2 ,., y n corresponding to x= x 0 , x 1 , x 2 , x n That is y i = f(x i
Suppose, we have a table of data with four pairs of x and f (x) values. With x; indexed by variable ‚i‘: Here, we do not assume uniform spacing between the x-values, nor we need the x-values
Lagrange Interpolation: Constructs an interpolating polynomial through the data points using the polynomial of the same name. It can be used for polynomials of any degree
Example No 1: Interpolate the value of the function corresponding to X = 4 X = 4 using Lagrange’s interpolation formula from the following set of
• The interpolation points or nodes are given as:: • There exists only one degree polynomial that passes through a given set of points. It’s form is (expressed as a power series): where =
- Lagrange Interpolation Formula: Definition, Properties, Uses
- Videos von Examples of lagrange interpolation
- Lagrange Interpolation Method Algorithm
- Chapter 8 Numerical Differentiation Integration
- Interpolation and the Lagrange Polynomial
LECTURE 5 HERMITE INTERPOLATING POLYNOMIALS
The advantages of Lagrange Interpolation are: The Lagrange Interpolation formula is simple and easy to remember. The application of the Lagrange Interpolation formula is not swift. The
Lagrange’s Interpolation. In Lagrange’s Interpolation, we only know the values of variables and there is no function given for it. It works for both spaced and unequal spaced
Newton’s forward interpolation formula given by:, , , Also from table , , Substituting these values in , we get Also 7.2.2 Newton’s Backward Interpolation Formula Newton’s backward interpolation
Lagrange interpolation is a well known, classical technique for interpolation . It is also called Waring-Lagrange interpolation, since Waring actually published it 16 years before Lagrange [
There are different methods for interpolation for example: Newtons Forward Interpolation, Netwtons Backward Interpolation, Newtons General Interpolation with divided difference,
Inverse Interpolation: Lagrange formula •On the other hand, the process of estimating the value of x for a value of y is called inverse interpolation. •When the values of y are unequally spaced,
The Lagrange Interpolation Formula finds a polynomial called Lagrange Polynomial that takes on certain values at an arbitrary point. It is an nth-degree polynomial expression of

Lagrange Interpolating Polynomials Definition Let {x 0,x 1,,x n}be a set of n + 1 distinct points at which the function f(x) is defined. The (unique)Lagrange Interpolating Polynomial of f(x) of
Examples Polynomial interpolation Piecewise polynomial interpolation Lagrange interpolating polynomial I General form of the Lagrange polynomial interpolation L n(x) = y 0l 0(x) + y 1l 1(x)
3.1. POLYNOMIAL INTERPOLATION Call P. N. the space of real-valued degree-Npolynomials: N. P. N = f X a. n. x. n: a. n n=0. 2Rg: Lagrange’s solution to the problem of polynomial
Lagrange Frequency Response Examples . The following examples were generated using Faust code similar to that in Fig.4.12 and the faust2octave command distributed with Faust.. Orders 1
Interpolation, Extrapolation & Polynomial Approximation Kostas Kokkotas November 11, 2019 Eberhard Karls University of Tubingen 1. Introduction In many cases we know the values of a
A, or for an entire function f, we have f(A) = Q(A) where Qis the Lagrange interpolation polynomial of fwith interpolation points given by the eigenvalues of A. Explicit examples of using Lagrange
3.2.1: Lagrange Polynomial. THE LAGRANGE POLYNOMIAL; 3.2.2: Newton interpolation. NEWTON INTERPOLATION; 3.2.3: Cubic Splines; Given a set of data,
Barycentric Lagrange Interpolation Brian Caravantes Course: Math 4401 Numerical Methods Faculty: Barry McQuarrie University of Minnesota, Morris Fall 2016 ABSTRACT This paper will
The Lagrange interpolation formula can be used to determine the missing values, to construct a quadratic or polynomial equation from the given data. Let y = f(x) be a function such that f(x)
Lagrange’s Interpolation Formula with Solved Example. From Given set of data points evaluate f (x) using lagrange interpolation formula.
- L Zeichen Mit Fester Bedeutung
- Axcrypt 2.0 And 1.7 | Axcrypt Download Free
- Welcher Arzt Bei Bauchdeckenbruch
- All Minecraft Potions And Their Recipes Revealed
- Wemding: Nach Scheinimpfungen In Wemding Übernimmt Dr.
- ادبیات فارسی – فرهنگستان خط Farsi
- Stadtsportverband Paderborn Setzt Aufs Bewährte Team
- Wie Becquerel Die Radioaktivität Entdeckte
- Homebridge Version Update · Issue
- Xtherm Winter Suit
- Achieving Consistency In Ux Design: A Comprehensive Guide