Deriving Inverse Matrix Formula

Di: Everly

Discovering Matrix Inverse Formulas Once a matrix inverse formula is known, it is easy to check that it is true: we just multiply the two matrices together to verify that the result is the Identity

Videos von Deriving inverse matrix formula

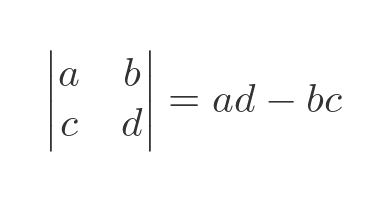
Appendix D: MATRIX CALCULUS D–2 In this Appendix we collect some useful formulas of matrix calculus that often appear in ﬁnite element derivations. §D.1 THE DERIVATIVES OF

What is the derivation for formula of inverse matrices (3×3 matrix) – algebraically derive the formula?

Linear Algebra: Formula for 2×2 inverse Figuring out the formula for a 2×2 matrix. Defining the determinant.

So the gradient of the inverse matrix with respect to itself is an order-4 tensor whereby every combination of elements of the inverse are multiplied together. This is similar to

Derivatives of inverse matrix
Deriving the inverse of a 2×2 matrix
Matrix Formula Derivation
Linear Algebra: Matrix Inverse

Inverse Matrix Calculator

Free derivative calculator – differentiate functions with all the steps. Type in any function derivative to get the solution, steps and graph

How to find the inverse of a 2×2 matrix using a formula

BlockMatrixFormulas.tex 7/7/2015,7/24/2015,November23,2024 and Φ= 0 −1 0 0 Θ −1 0 . (3) ThendetΦ=det detΘ,andweseethatgiven isinvertible,Φisinvertibleifand

Deriving System Y and Z Matrices. Underground Cables. Overhead (Aerial) Conductors The analysis of both overhead lines and underground cables begins with two well-known equations,

2. Formulas for the Drazin inverse of a modifiedmatrix dealing with the generalized Schur com- plement In this section, we present some formulas for the Drazin inverse of the

Matrix derivatives cheat sheet Kirsty McNaught October 2017 1 Matrix/vector manipulation You should be comfortable with these rules. They will come in handy when you want to simplify an

To calculate inverse matrix you need to do the following steps. Set the matrix (must be square) and append the identity matrix of the same dimension to it. Reduce the left matrix to row

Deriving System Y and Z Matrices
Deriving inverse matrix formula
How to derive the following formula for the inverse of a matrix?
Matrix Inverse Identities Statistical Machine Learning Veronica Burt
derivative of inverse matrix by itself

We need to find inverses of matrices so that we can solve systems of simultaneous equations. (We’ll see how to solve systems in the next section, Matrices and Linear Equations). We’ll find the inverse of a matrix using 2

The inverse of Matrix for a matrix A is A^-1. The inverse of a matrix can be found using a simple formula (adj A) / |A|. Learn about the matrix inverse formula for the square matrix of order 2 × 2 and 3 × 3 using solved examples.

Leontief Inverse Matrix (or Total Requirements Matrix) is a central mathematical object in Input-Output Analysis. The matrix represents the amount of gross output from sector i that is

DERIVATIVE OF THE MATRIX INVERSE ERIC PETERSON Consider the normed vector space L(Rn;Rn) of all linear operators of type signature Rn!Rn. Among these, there is an interesting

The easiest way to get the derivative of the inverse is to derivate the identity I = KK − 1 respecting the order (I) ′ ⏟ = 0 = (KK − 1) ′ = K ′ K − 1 + K(K − 1) ′. Solving this equation with respect to (K

I’ve already read another answer here: Deriving inverse matrix formula. However, this only covers $2\times 2$ matrices, disappointingly. I have checked Wikipedia and it has

The formula for the inverse of a $2×2$ matrix is: $A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$ If $\text{det}(A) = 0$, the matrix has no inverse.

We use this formulation to define the inverse of a matrix. Let A be an n × n (square) matrix. We say that A is invertible if there is an n × n matrix B such that. AB = I n and BA = I n . In this

The proof that your expression really is the inverse of $\;A\;$ is pretty easy. How it is derived can be done as follows without deep knowledge in matrix theory:

The n.th power of a square matrix A 1 The inverse matrix of the matrix A A+ The pseudo inverse matrix of the matrix A (see Sec. 3.6) A1=2 The square root of a matrix (if unique), not

How to derive the inverse matrix: Start with the augmented matrix $$\left(\begin{array}{cc|cc} a & c & 1 & 0 \\ b & d & 0 & 1\end{array}\right)$$ and perform

j-th column $v$ of inverse matrix should satisfy equation: $$A v = e_j$$ Where $e_j$ is j-th vector of canonical basis. So apply Cramer’s rule to this equation and compare it with what you want

$\begingroup$ Dear @rcollyer: Thanks for your interest. I don’t really know a convenient reference for this, but it’s so simple that it’s easier to describe (and prove) the statements.

Can any one help me in deriving the matrix inversion lemma rule for RLS algorithm? I don’t know how to start with. Many books have just stated but they haven’t derived

DEFINITION The matrix A is invertible if there exists a matrix A−1 that “inverts” A: Two-sided inverse A −1 A = I and AA −1 = I. (1) Not all matrices have inverses.

OLS in Matrix Form 1 The True Model † Let X be an n £ k matrix where we have observations on k independent variables for n observations. Since our model will usually contain a constant

Matrix Calculus From too much study, and from extreme passion, cometh madnesse. −Isaac Newton [205, § 5] D.1 Gradient, Directional derivative, Taylor series D.1.1 Gradients Gradient

The inverse matrix is then: R leading to the rather ugly general formula: Rˆ(φ,θ,ψ) = cosψcosφ−cosθsinψsinφ −sinψcosφ−cosθsinφcosψ sinθsinφ cosψsinφ+cosθcosφsinψ

Derivative of the inverse of a symmetric matrix w.r.t itself Hot Network Questions Why doesn’t visudo, like sudoedit, spawn a text editor as a regular user?

Alternative names for this formula are the matrix inversion lemma, Sherman–Morrison–Woodbury formula or just Woodbury formula. However, the identity appeared in several papers before the

GORT

Reviews