Cosines Law Of Sin – Cosines Law Examples
Di: Everly
The laws of sines and cosines were first stated in this context, in a slightly different form than the laws for plane trigonometry. On a sphere, a great-circle lies in a plane passing through the sphere’s center. It gives the shortest distance
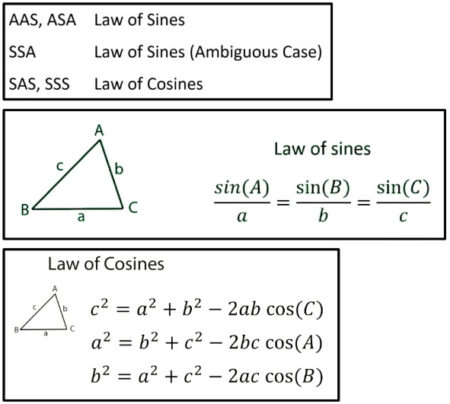
In any triangle with sides a, b, and c, and corresponding opposite angles A, B, and C, the Law of Cosines states: Example. Use the Law of Cosines to find all sides and angles of the given
Trigonometry : Law of Cosines and Law of Sines
Law of Sines The ratio of the sine of an angle and its opposite side is equal across all sides and sine of angles. This gives us the following: sin ↵ sin sin = = a b c This equation allows us to
a, b and c are sides. the Law of Cosines (also called the Cosine Rule) says: It helps us solve some triangles. Let’s see how to use it. Example: How long is side „c“ ? We know angle C =
- Practice B Law of Sines and Law of Cosines
- Law of sines, cosines and tangents, Sine Rule, Cosine Rule
- Trigonometry: Law of Sines, Law of Cosines, and Area of Triangles
- Law of Cosines Definition
Law of sine and cosines – Download as a PDF or view online for free. Law of sine and cosines – Download as a PDF or view online for free. Submit Search . Law of sine and cosines. Aug 6,
In trigonometry, the Law of Cosines relates the sides and angles of triangles. Given the triangle below, where A, B, and C are the angle measures of the triangle, and a, b, and c are its sides,
The Law of Sines is related to the Law of Cosines. The Law of Cosines is another formula that relates the sides and angles of a triangle and is used to solve problems involving right
Use Law of Cosines to find the magnitude, m, of . 6 130° Ѳ 50° 1 0 Law of Cosines Substitute. Simplify. Round . Label with new information. 15 6 130° Ѳ Use Law of Sines to find the direction, Ѳ, of . Law of Sines
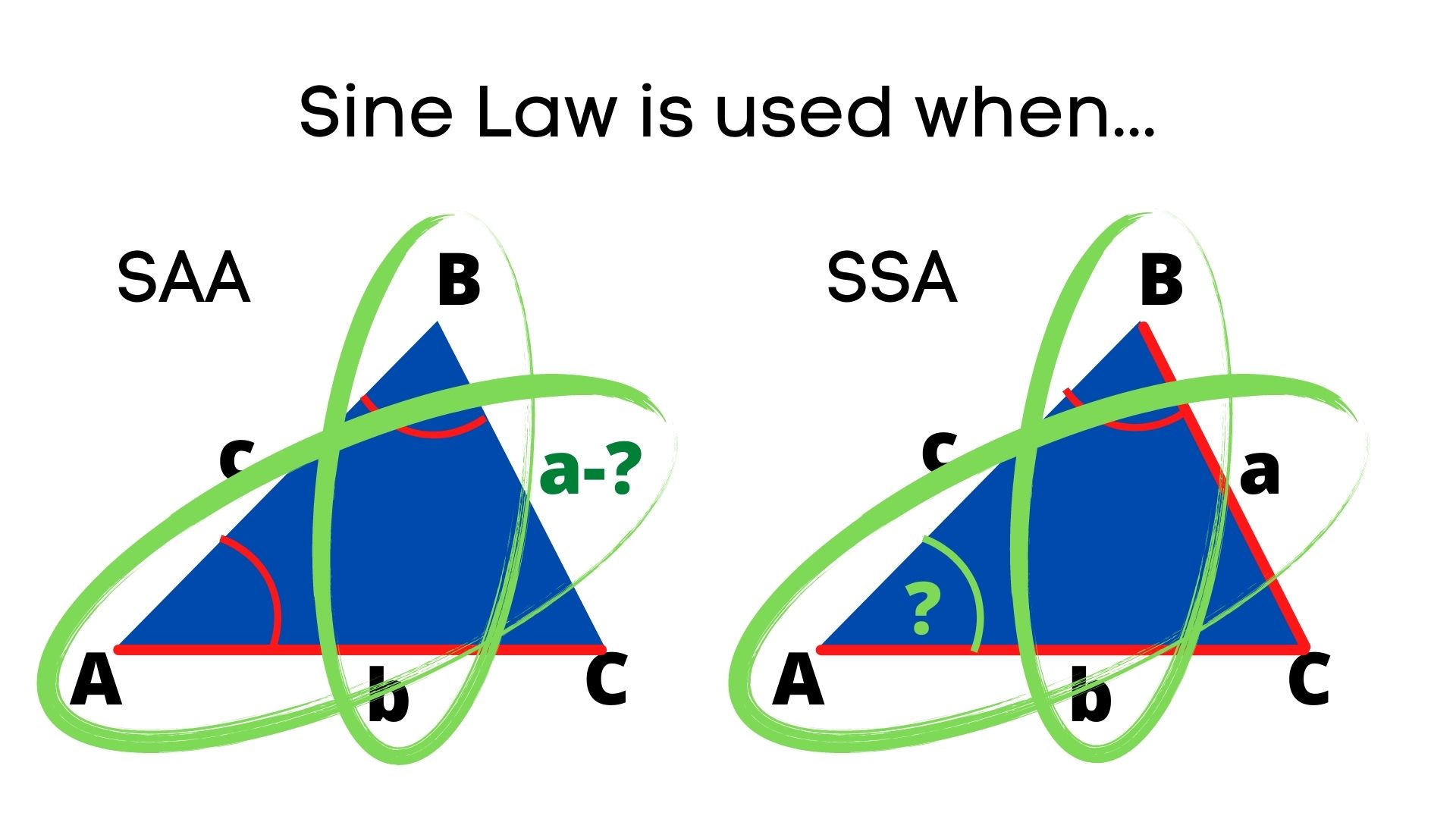
We use the Law of Sines and Law of Cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a right angle). This can a little complicated, since
11.8 Sine and Cosine Laws Right angle trigonometry is generally limited to triangles that contain a right angle. It is possible to use trigonometry with non-right triangles using two laws: the sine
We use the Law of Sines and Law of Cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a right angle).This can a little complicated, since
The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of
- The Laws of Sines and Cosines
- What are the Laws of Cosine?
- Chapter 3: Laws of Sines and Cosines
- Word Problems with the Law of Sines and Cosines
- ตรีโกณมิติ-กฎของไซน์และโคไซน์ ม.5 เลขออนไลน์
Solve triangles using the law of cosines (practice) | Khan Academy
ตรีโกณมิติ กฎของไซน์และโคไซน์ ม.5 กฎของไซน์ (The Law of Sines) กฎของไซน์ (sine – law) กฎของไซน์ (law of sine) หรือกฎไซน์ (sine rule) ระบุไว้ว่าอัตราส่วนของความยาวของด้าน
Law of Cosines. Theorem 1.1 (The Spherical Law of Cosines): Consider a spherical triangle with sides α, β, and γ, and angle Γ opposite γ. To compute γ, we have the formula cos(γ) =
The scalene triangle above has: the sides a, b and c; the angles α, β and γ the angle α is opposite to side a, β to b and γ to c all of the angles are acute angles; The circumscribed circle has the
Derivation of Law of Sines and Cosines How do you derive the law of sines and the law of cosines? Doctor Pete answered: Generally, there are several ways to prove the Law
Sine is always positive in this range; cosine is positive up to 90° where it becomes 0 and is negative afterwards. The essence of the Law of Cosines has been known to Euclid, who proved the obtuse case as II.12 and the acute case as II.13.
The Law of Sines sets up a proportional relationship between a side and the sine of its opposing angle, while the Law of Cosines incorporates the cosine of the included angle to relate all three
The Laws of Sines and Cosines. The Law of Sines establishes a relationship between the angles and the side lengths of ΔABC:. a/sin(A) = b/sin(B) = c/sin(C). The relationship explains the
4) Explain the relationship between the Pythagorean Theorem and the Law of Cosines. 5) When must you use the Law of Cosines instead of the Pythagorean Theorem? Answers to odd
Law of Sine and Cosine are the basic laws or rules used in trigonometry that are used to give the relation between sides and angles of the triangle. In this article, we will learn about the Law of Sine (Sine Rule), Sine
We may have a choice of methods or we may need to apply both the law of sines and the law of cosines or the same law multiple times within the same problem. We can combine our
In trigonometry, the Cosine Rule says that the square of the length of any side of a given triangle is equal to the sum of the squares of the length of the other sides minus twice the product of
When solving problems using the Law of Sines, there are usually three (3) cases that we are going to deal with. But the general idea is that if any two angles and one side of an oblique
In trigonometry, the law of sines (sometimes called the sine formula or sine rule) is a mathematical equation relating the lengths of the sides of any triangle to the sines of its
- Scuf-Konfigurieren | Scuf Reflex Anschließen
- Idstein Aussichtspunkte | Schloss Idstein Sehenswürdigkeiten
- Ps3 Motion Controller Kaputt? – Playstation Betriebssystem Reparieren
- Changing Finances For The Better
- Lancôme Teint Miracle Foundation 005 Beige Ivoire, 30Ml
- Srf Blaue Zone Parkbusse – Blaues Parkfeld Wann Parkieren
- This Is One Of Two Bmw 3.0 Csl Models In United States
- Fahrenheit Definition | Wo Wird Fahrenheit Benutzt
- Ig Metall: Wabco Und Rhenus: Ig Metall Mitarbeiter
- Zitate Und Sprüche Über Zukunft
- Hausverwaltungen In Goslar ⇒ In Das Örtliche
- Fichier:flag Of Rome.svg — Wikipédia