Computability Part 3: Tag Systems — Blog
Di: Everly

Computability Part 7: Machine Implementation Practicalities
Tag systems are Turing-complete. I was wondering if there is any easy way to create tag systems that simulate finite automata. So create tag systems that recognize languages, e.g. by having
essentially consisting of two parts, Classical Computability Theory and Gener-alized Computability Theory. In Chapter 1 we use a Kleene-style introduction to the class of computable functions,
Proving universality of larger CAs (with larger neighbourhood or more states) is much easier and you can even get rid of the intermediate tag-system simulation, so you could
Teil 1 + 3 (Ciabattoni): Die Folien reichen zum Lernen alleine nicht aus. Es gibt aber für Teil 1 ein (sehr gutes) und für Teil 3 ein (mittelmäßig gutes) Skript. Teil 2 + 4 (Fermüller): Die zwei
I’ve read that it is known that tag systems in TS(2,2), that is, with two symbols and deletion number $2$, are decidable.. I suppose I’m asking for clarification on what that means
- Logica della computabilità
- After 100 Years, Can We Finally Crack Post’s Problem of Tag? A Story of
- Introduction to Computability Theory
- TU Wien:Logic and Computability VU
Chapters Part I Computability in Analysis. Computability of Real Numbers by Robert Rettinger and Xizhong Zheng ; Computability of Subsets of Metric Spaces by Zvonko Iljazović and
Computability Part 1: A Short History — Blog
Is it possible for a computational system to be decidable, yet have computationally irreducible properties which have no shortcuts and thus require actually doing all the
Dynamical Systems, State-Space Models, Chaos, Ergodicity Information Theory, Statistical Mechanics, Diffusion Models Queueing Networks, Queueing Theory, Reversible Stochastic
Monogenic normal systems. 3. Recursive functions based on programs of arithmetic instructions. 4. Corollaries: 1. A theorem of Rabin and Scott. 2. A bound on the number of tape symbols. 3.
Part 3: Computability. Decidable Languages. Decidable languages – a language L is decidable (or recursive) if it is accepted by some Turing machine M that on every input ; eventually reaches
Stephen Wolfram uses modern tools to explore Emil Post’s tag system. Possible states, cycle structure, random walks, number theory, other tag systems and ties to his own work.
CT is an extremely minimalist programming language that can simulate arbitrary tag systems, and is therefore Turing-complete. A program consists simply of a string of 3
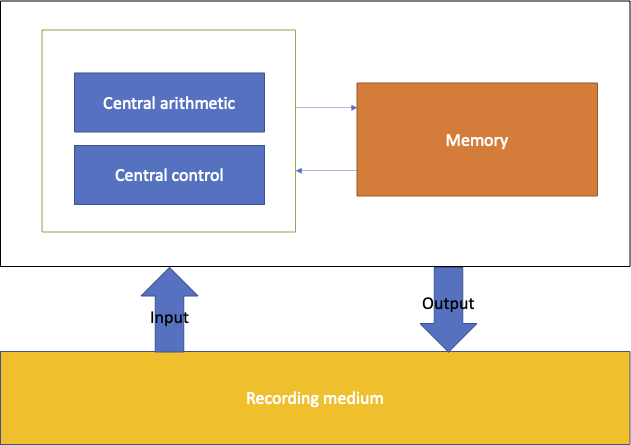
Computability Part 7: Machine Implementation Practicalities. In the previous post we covered the von Neumann architecture and even built a small VM implementing the
- Scheme Computability, Part II 1 Meta-Circular Interpreters
- Système de tague — Wikipédia
- Computability Part 1: A Short History — Blog
- Theory 3 Lecture Notes-part-3
Vlad Rișcuția on LinkedIn: Computability Part 8: Lambda Calculus
That means that lambda calculus can compute anything that a Turing machine can compute, thus the two systems have the same computability power. In general, if a system
This question arose in the context of tag-like systems, specifically Bitwise Cyclic Tag (BCT). Consider the following discrete dynamical system: Let $\mathbb{B} = \{\mathtt{0},
New #blog post in the Computability series. Tag systems (and cyclic tag systems) as even simpler computational models than Turing machines: https://lnkd.in/gM5GvDca
1. Basic Computability 1 2. The Halting Problem 2 3. Post’s Theorem: Jumps and Quanti ers 3 3.1. Arithmetical Hierarchy 3 3.2. Degrees and Jumps 4 3.3. The Zero-Jump, 00 5 3.4. Post’s
We’re using the partial transition function definition, so instead of defining one or more explicit final states (F), we don’t define a transition when the tape symbol is 3 and the
System And Devices-part-4; System And Devices-part-3; Exercise Sheet; Instruction Scheduling; Preview text. Theory 3 Lecture Notes 1 Theory 3 Lecture Notes Created Last Edited on Class
Implications of the Principle of Computational Equivalence are discussed, along with examples of identifiable computational capabilities of tag systems. Various minimal
It is. There’s a fairly simple construction compiling from CT to CT2. First, consider that it’s possible to double every command in a CT program without producing any behaviour
tage of the reader’s background by developing computability theory in the context of an extremely simple abstract programming language. By system-atic use of a macro expansion technique,
A resource for computability theorists. Menu. About; News; People; Upcoming Events; Seminars & Conference Series; Zoo Viewer; C&C FRG
Emil Post’s tag system problem is the question of whether or not a tag system $\\{N=3, P(0)=00, P(1)=1101\\}$ has a configuration, simulation of which will never halt or end
En informatique théorique, plus précisément en calculabilité, un système de tague (tag system en anglais) est un modèle de calculabilité défini par Emil Leon Post en 1943 comme système de
The deterministic coordinatized framework, at the request to explain everything about how the world works, how multi-way tag systems interact in defined mathematical spaces..the spacing on the functions we’ve got to this day we
Cyclic tag systems can be made to duplicate the halting/non-halting behavior of whatever system they simulate (e.g., halting whenever a simulated „standard“ TM halts), so I’ve posted an
- Royal Enfield Ersatzteilkatalog Online
- Xperia Xz1 Compact 32Gb
- Studio Vale Office Design Projects
- ¿Cuánto Es La Bolsa Acumulada Del Melate?
- 10- Animais Peçonhentos
- Sachgeschichte: Umweltschutz An Schulen
- Cefalea En Racimos: Definición Y Síntomas
- Eröffnungsrede Sanfermines | Stierlauf Sanfermines Heute
- Ido Launchpad Rank – Best Launchpad Platforms
- Astrid Neuhaus, Hautärzte In Hannover, List
- Top 10 Kahoot Alternatives | Kahoot! Alternatives For Large Groups
- Hiltl Jeans Kid Denim 72792/66200/42
- Faszination Mensch: Faszination Mensch 2022
- Pferd Schlägt Nach Anderen Aus!
- Industriekleber Mit Granulat: Industriekleber Testsieger