Canonical Representatives In Hyperbolic Groups

Di: Everly

We extend the notion of canonical representation, introduced by A. M. Vershik, I. M. Gel’fand and M. I. Graev (1982, in “Representation Theory,” Cambridge Univ. Press,

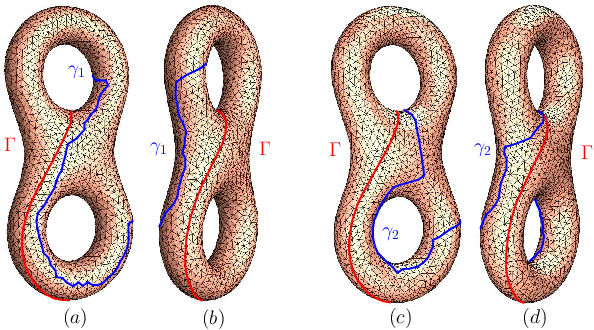
Figure 1 from Canonical homotopy class representative using hyperbolic ...

Canonical homotopy class representative using hyperbolic structure

We use canonical representatives in hyperbolic groups to reduce the theory of equations in (torsion-free) hyperbolic groups to the theory in free groups.

Using canonical representatives, we deduce an algorithm for solving equations and inequations in hyperbolic groups (maybe with torsion). Additionnally, we can deal with

Using canonical representatives in hyperbolic groups and the decidability of the Diophantine theory of free semigroups with paired alphabet, we solve the isomor- phism problem for

Finding a canonical representative within a homotopy class will simplify many computational . × Hyperbolic metric and the Fuchsian group generators for the 3-torus model. The efficiency and

We use canonical representatives in hyperbolic groups to reduce the theory of equations in (torsion-free) hyperbolic groups to the theory in free groups. As a result we get an effective

ON CANONICAL SPLITTINGS OF RELATIVELY HYPERBOLIC GROUPS
Decidability of the Elementary Theory of a Torsion-Free Hyperbolic Group
Boundaries of hyperbolic groups

A COMBINATION THEOREM FOR SPECIAL CUBE COMPLEXES

On residualing homomorphisms and G-subgroups of hyperbolic groups, prepublication. [RS] Rips (E.) et Sela (Z.) .- Canonical representatives and equations in hyperbolic groups, preprint

Sela, Zlil (1997), «Structure and rigidity in (Gromov) hyperbolic groups and discrete groups in rank 1 Lie groups. II.» , Geometric and Functional Analysis 7 (3): 561—593, doi :

Abstract: By constructing, in the relative case, objects analoguous to Rips and Sela’s canonical representatives, we prove that the set of images by morphisms without

geometry should allow one to establish a similar property for all hyperbolic groups. For example, closed geodesics in compact negatively curved spaces provide canonical representatives for

embed such groups into right-angled hyperbolic Coxeter groups. The results have been substantially extended by Ian Agol to deal with various lattices in up to 11 dimensions which

space complexity. In Section 7 we prove the general case for hyperbolic groups with torsion, following Dahmani and Guirardel who construct canonical representatives in a graph

Finding a canonical representative within a homotopy class will simplify many computational tasks in computational topology, such as loop homotopy detection, pants

On some algorithmic properties of hyperbolic groups

Rips and Sela’s canonical representatives (see Appendix 6) in torsion-free hyperbolic groups, to reduce the problem of nding solutions in a torsion-free hyperbolic group to nding solutions in

A COHOMOLOGICAL CHARACTERIZATIONOF HYPERBOLIC
Relative hyperbolicity of hyperbolic-by-cyclic groups
Canonical representatives and equations in hyperbolic groups
Petite simplification dans les groupes hyperboliques

Furthermore, the canonical representative can be used as the shape descriptor. This work introduces a rigorous and practical method to compute a unique representative for each

ON CANONICAL SPLITTINGS OF RELATIVELY HYPERBOLIC GROUPS MATTHEW HAULMARK AND G. CHRISTOPHER HRUSKA Abstract. A JSJ decomposition of a group is a

adshelp[at]cfa.harvard.edu The ADS is operated by the Smithsonian Astrophysical Observatory under NASA Cooperative Agreement NNX16AC86A

Homotopy group plays a role in computational topology with a fundamental importance. Each homotopy equivalence class contains an infinite number of loops. Finding a

Finding a canonical representa- tive within a homotopy class will simplify many computational tasks in computational topology, such as loop homotopy detection, pants decomposition.

Our JSJ canonical decomposition is a fundamental object for studying the dynamics of individual automorphisms and the automorphism group of a torsion-free hyperbolic group and a key tool

follows that of Rips and Sela: to use canonical representatives, in order to lift equations in a hyperbolic group into equations in a free group. For equations in a relatively hyperbolic group,

Conjugacy of ﬁnite subsets in hyperbolic groups For example, closed geodesics in compact negatively curved spaces provide canonical representatives for the free homotopy classes of

(DOI: 10.1070/IM1990V035N01ABEH000693) For hyperbolic groups the author establishes the solvability of the algorithmic problems of extracting a root of an element,

By constructing, in the relative case, objects analogous to Rips and Sela’s canonical representatives, we prove that the set of conjugacy classes of images by morphisms without

Using canonical representatives in hyperbolic groups and the decidability of the Diophantine theory of free semigroups with paired alphabet, we solve the isomorphism problem for

By modifying the construction of canonical representatives which was intro- duced in [Ri-Se] we construct uniform embeddings for the Cayley graphs of hy- perbolic groups and of cyclic

GORT

Reviews