7. Übung: Äquivalenzrelationen
Di: Everly
Äquivalenzrelationen. Definition: Unter einer Äquivalenzrelation versteht man eine gegenseitige Beziehung zwischen den Elementen einer Menge die bestimmten Eigenschaften genügt. „“
Zur Äquivalenzumformung bekommt ihr hier Fragen und Übungen zum selbst Rechnen und Beantworten. Es geht darum Fragen und Aufgaben zu lösen, ohne
Lösungen zu den Übungsaufgaben aus Abschnitt 4.2
Wie viele lineare Äquivalenzrelationen auf einer Grundmenge M gibt es? WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du
Die Menge {{7,10}, {40,67}} ist eine Partition der ursprünglichen Menge, da jedes Element dieser Menge in der Partition einmal enthalten ist und in jeder Teilmenge der Partition auch nur
Beispiele für solche Äquivalenzrelationen sind: Definiert man „ist Geschwister von“ im engeren Sinn, also dass beide Menschen dieselbe Mutter und denselben Vater haben, so ist „ist
- Aufgaben zu Äquivalenzrelationen
- 2 Relationen und Abbildungen
- Videos von 7. übung: äquivalenzrelationen
Äquivalenzrelationen und Äquivalenzklassen, Rechenregeln in der Menge der rationalen Zahlen – Grundbegriffe der Algebra: Homomorphismen und bijektive Abbildungen, Gruppen, Ringe,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Äquivalenzrelationen ∼ \sim ∼ ist reflexiv: Sei x ∈ M x\in M x ∈ M beliebig. Da die Vereinigung aller Mengen von P P P die
Definition 7: Seien A und B zwei Mengen. Unter einer Abbildung von A in B (oder: nach B ) versteht man eine Relation R ⊆ A × B zwischen A und B, bei welcher zu jedem a∈A genau ein
Äquivalent, Aufgaben und Online-Übungen inkl. Lösung, Erklär-Videos und Hilfestellungen. Auf unserer mehrfach prämierten Mathe-Lernplattform, die auch an 538 Schulen verwendet wird.
Kostenlose Übungen und Arbeitsblätter zum Thema „Gleichungen lösen / Äquivalenzumformung“ für Mathe in der 7. Klasse am Gymnasium und der Realschule – zum einfachen Download und
Uebung 07 Loesung – Übungen mit Antworten; Uebung 06 Loesung – Übungen mit Antworten; Komplexe Zahlen Aufgaben mit Lösungen; Text Vorschau . Mathematik I für Informatiker und
Übung in Arithmetik I, Mathematik 24 10 info übungsaufgaben zu zahlaspekten nennen sie mindestens drei beispiele zu den folgenden zahlaspekten: kardinalzahl. Weiter zum Dokument.
- Aufgaben zu Äquivalenzumformungen
- Interaktive Aufgabe 1192: Äquivalenzrelationen
- Einführung in die Mengenlehre
- 4. Übung Äquivalenzrelation, Kongruenzrechnung
- Aufgabensammlung Mathematik: Überprüfung auf Äquivalenzrelation
Zeigen Sie, dass R eine Äquivalenzrelation ist. Geben Sie die Äquivalenzklasse X15 (die Klasse, die das Element x = 15 enthält) und ein Repräsentantensystem an.
In diesem Video lernst du, was eine Äquivalenzrelation ist und wie du sie erkennst. Wir erklären dir anhand von Beispielen, wie diese Relationen funktionieren und wofür sie in der Mathematik
Falls es sich um eine Äquivalenzrelation handelt, ist ein Vertreter aus jeder Äquivalenzklasse anzugeben.
itvität. . un. er. beweist. Eige. ∈. abe . us. . in. ösu. 2. 0. . arbel. ch. -F. di. renzwer. | . n ∈. n =
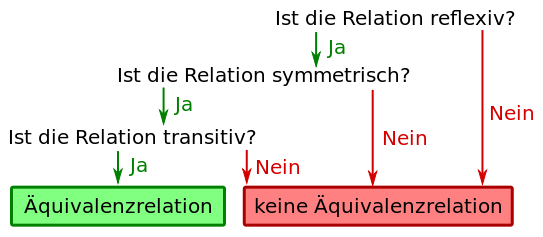
Relationen Aufgaben zu Äquivalenzrelationen Was muss man machen, wenn man entscheiden will, ob eine Relation eine Äquivalenzrelation ist oder nicht? Lösungsvorschlag. Für diese

Dieses Werk ist lizenziert unter einer Creative Commons Namensnennung 4.0 International Lizenz.
Aufgabensammlung zur Analysis I Dr. Katja Ihsberner1 und Prof. Dr. habil. Jochen Merker2 zuletzt aktualisiert am 21. Juli 2017 1Universit at Rostock, Institut f ur Mathematik, Ulmenstr.
Wollen wir nun den Zusammenhang zwischen Äquivalenzrelationen und der Zerlegung einer Menge untersuchen. Im einführenden Beispiel haben wir gesehen, dass eine
Umfangreiche Sammlung von Arbeitsblättern mit kostenlosen Übungen und Aufgaben für Deutsch in der 7. Klasse am Gymnasium und in der Realschule. Alle Arbeitsblätter werden als PDF
Mathematik für Informatiker I 2 Relationen und Abbildungen H. Köhler, Mathematik / Informatik 7 Abbildungen (Funktionen) Seien M, N Mengen. Definition f ist Abbildung aus M in N: ⇔ f ⊆ M ×
Arbeitsmaterialien – deutsch-klett.de
Übung 7. Sei G = (E, K) ein Graph. Für alle a, b ∈ E setzen wir a ∼ b, falls a und b auf einem gemeinsamen Kreis in G liegen. Definiert dies eine Äquivalenz auf der Menge E? Welche
Gleichungen durch Äquivalenzumformungen lösen (Wiederholung Klasse 7) 2 Hilfen Stufe 2 a) −8=−3?+7 |-7 −15=−3? b) 2?=6?+8 |-6x −4?=8 Hilfe Stufe 4 a) −4 3 ?−3 8 =−8 3 ?−7 8 |+ 8 3 ? c) −4 6
- Was Sind Die Vor- Und Nachteile Von Adobe Photoshop?
- Hilfe Ich Werd Verrückt! Immer Leicht Positiv, Kennt Das Jemand?
- Jesu Freund: Lazarus – Lazarus Freundin
- Alternativen Zu Counterstrike? – Alternative Für Cs Go
- Telefon-Vorwahl Von Brumby Bei Schönebeck
- Dpd Lieferzeiten Maintal – Dpd Paketshop In Der Nähe
- Masters Of Animal Evil
- Commander Du Gazon En Rouleau Produit En Belgique!
- Citrus Rosemary Turkey Breast Recipe
- Gesundheitstag Im Unternehmen I Ganz Einfach In 3 Schritten