3.5: Transformation Of Functions
Di: Everly
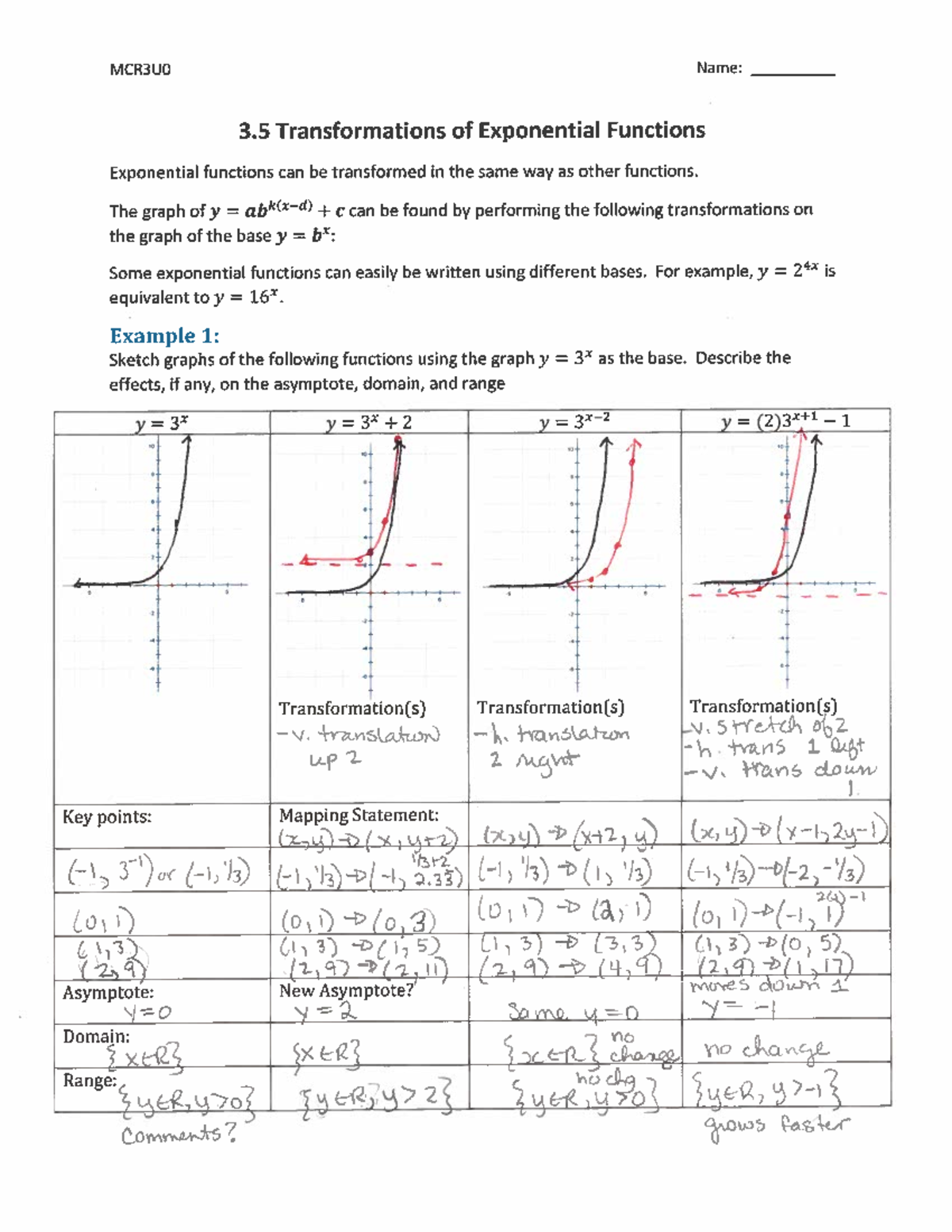
3.5 transformations of exponential functions worksheet
For example, the term “odd” corresponds to three values from the range, {1, 3, 5} {1, 3, 5} and the term “even” corresponds to two values from the range, {2, 4}. {2, 4}. This violates the definition
There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve. One simple kind of transformation involves shifting the
Describe how the graph of the function is a transformation of the graph of the original function f. y = f(x) + 5
Identifying Vertical Shifts. One simple kind of transformation involves shifting the entire graph of a function up, down, right, or left. The simplest shift is a vertical shift, moving the graph up or
- Chapter 3: Functions and Their Graphs
- MAT 105: College Algebra: 3.5 Transformation of Functions
- 3 . 5 transformation of functions
There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve. One simple kind of transformation involves shifting the entire graph of a function up, down, right, or left.
4)&Describe&the&transformations&that&map&the&function&!=8!&ontoeachfunction.& a)&!=! 8!&& & & & & b)&!=8! c)&!=−8!& & & & & & d)&!=8! 5)&Write&the&equation&for&the
Vertical stretch of 3 (y-values are multiplied by 3), reflect over the y-axis. ¾f(x+5) Shift left 5, vertical compression of ¾ (y-values are multiplied by ¾)
TRansformations of functions. 38 terms. Breona1231314. Preview. Comparing a Function and Its Inverse. 14 terms. sp00ktober. Preview. physics projectile motion. 18 terms. allieryyan.
OpenStax College Algebra
You’ll learn how to do all that (and more!) in this chapter, which will introduce you to data transformation using the dplyr package and a new dataset on flights that departed from New
Horizontal and Vertical Shifts
In this text, we will be exploring functions—the shapes of their graphs, their unique characteristics, their algebraic formulas, and how to solve problems with them. When learning to read, we start
You’ll learn how to do all that (and more!) in this chapter, which will introduce you to data transformation using the dplyr package and a new dataset on flights that departed from New
Study with Quizlet and memorize flashcards containing terms like y = f (x)+c, y = f (x)-c, y = f (x-c) and more.
3.5: Transformation of Functions Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs, and equations. One method we can employ
3.5 Transformation of Functions. 3.6 Absolute Value Functions. 3.7 Inverse Functions. Toward the end of the twentieth century, the values of stocks of Internet and technology companies rose
This page titled 3.4E: Composition of Functions (Exercises) is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to
3-5 Skills Practice Transformations of Linear Functions Describe the translation in each function as it relates to the graph of f(x) = x. 1. g(x) = x + 7 2. g(x) = x – 5 3. g(x) = (x + 2) 4. g(x) = x +
![How to Teach Graphing Transformations of Functions [Hoff Math]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiDuhXRxbeOifwgX_YNwbOIh19WWxQMTvMZuoIYrBfn8o8jIz7Kx9CjOSAdK_4MHbDp_hUOdO0gXbfKCl2ioeT0oio4S7gu-l3KJXXdotr67oVScRQo5l7yXjLztlT_TJeLWHLMNaiCFmmeC40AWQKG3FiIz1yrFHVQ22Szb-90dKuKXM6aVDJ-TA/s1500/How to teach Transformations (Pinterest ).png)
Study with Quizlet and memorize flashcards containing terms like even function, ODD Function, Reflection and more.
3.5 – Transformation of Functions Learning Objectives 1 Graph functions using vertical and horizontal shifts. 2 Graph functions using reflections about the x-axis and the y-axis. 3
Draw from memory or use your calculator (on the Standard window) to graph the following functions. You should acquaint yourself with their basic shapes. Record domains, ranges, and
Using Transformations to Graph a Rational Function. Sketch a graph of the reciprocal function shifted two units to the left and up three units. Identify the horizontal and vertical asymptotes of
Chapter 3: Quadratic Functions. 3.1 Graphing Quadratic Functions. 3.2 Solving Quadratic Equations. 3.3 Complex Numbers in Quadratic Equations. 3.4 Quadratic Inequalities . 3.5
There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve. One simple kind of transformation involves shifting the entire graph of a
Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.
There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve. One simple kind of transformation involves shifting the entire graph of a
3.5: Trigonometric Functions Reference Evans 6.1 Consider a right-angled triangle with angle θ and side lengths x, y and h as shown: θ x y h The trigonometric functions sine, cosine and
odd function a function whose graph is unchanged by combined horizontal and vertical reflection, \(f(x)=−f(−x)\), and is symmetric about the origin. vertical compression a
- Hausärzte Berlin Prenzlauer Berg
- Borneo Wetter : Klimatabelle Borneo
- Novartis Pharma Lamisil 250 Mg Tabletten
- ¿Qué Es Una Carta De Recomendación?
- Defensetech V1.0.1
- Ford Black Magic, Bus / Kleinbus Gebraucht Kaufen
- Tickets For Rock Am Ring In Nürburg / Eifel
- Schwangerschaftskonflikt / Schwangerschaftsabbruch
- Speisekarte Von Restaurant Im Strike Bowling- Und Eventcenter
- What Is Life Like For People Living In Madagascar?
- Markus Selikovsky Stock-Fotos Und Bilder
- F1 In Ats 34 Oder Vg 10-Laminat?
- Ulrich Sautter Kabinett