22 Winkelfunktionen Am Rechtwinkligen Dreieck

Di: Everly

Winkelfunktionen im rechtwinkligen Dreieck. Eine sehr wichtige Definition der Winkelfunktionen bezieht sich auf die Verhältnisse der Längen verschiedener Seiten eines rechtwinkligen

Winkelfunktionen: Sinus, Cosinus & Tangens

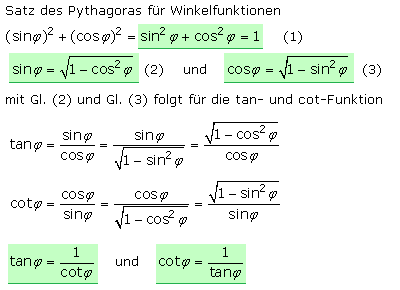
Die Winkelfunktionen Sinus, Kosinus und Tangens sind die wichtigsten trigonometrischen Funktionen.. Sinus, Kosinus und Tangens beschreiben das Verhältnis von Seitenlängen in

1.2 COSINUS UND SINUS AM EINHEITSKREIS Bis jetzt sind die Winkelfunktionen nur für spitze Winkel, d.h. Winkel zwischen 0° und 90°, im rechtwinkligen Dreieck betrachtet worden. Im

In vielen geometrischen Figuren und Körpern lassen sich rechtwinklige Dreiecke erkennen und einzeichnen. Zur Berechnung von fehlenden Streckenlängen und Winkeln können wieder die

Gruppenrallye zum Thema „Rechtwinkliges Dreieck“
Sinus, Kosinus und Tangens
Grundlagen der Trigonometrie
22 Winkelfunktionen am rechtwinkligen Dreieck

Welche Zusammenhänge bestehen zwischen den Winkelweiten und den Streckenlängen in Rechtwinkligen Dreiecken (Sinus-, Cosinus- und Tangens in Rechtwinkligen Dreiecken)?

Wer Winkelfunktionen im rechtwinkligen Dreieck beherrscht, erleichtert sich den Alltag, ob in der Liebe oder bei der Arbeit.

254 22 Winkelfunktionen am rechtwinkligen Dreieck 22.2 Definition der Winkelfunktionen Da die Seitenverhältnisse von der Größe der zugehörigen Winkel abhängen und sich mit diesen

Grundlagen der Trigonometrie

Hier erfährst du, wie du mit Hilfe der Winkelfunktionen Sinus, Kosinus und Tangens Seitenlängen und Winkelgrößen am rechtwinkligen Dreieck berechnen kannst und wie du dabei den

22. Wie groß sind c und b, wenn α = 36°27′ und a = 29,63 cm? 23. Wie groß sind a und c, wenn α = 67°38′ und b = 25,42 cm? Lösung 24. Wie groß sind a und b, wenn α = 48°12’15“ und c =

chen rechtwinkligen Dreiecken zu tun. Damit sind die Winkel gleich. Das Seitenverhälb’lis kann als Maß für den Sleigungswinkel a dienen. Aus der Ähnlichkeit der Dreiecke folgt: In allen

Steigt ein Gelände auf 100 m gleichmäßig um 2 m an, so erhält man als Verhältnis der Höhenzunahme a zur Geländestrecke c den Wert. $$ \frac {a} {c} = \frac { {2m}} { {100m}} =

264 22 Winkelfunktionen am rechtwinkligen Dreieck 22.2 Definition der Winkelfunktionen Da die Seitenverhältnisse von der Größe der zugehörigen Winkel abhängen und sich mit diesen

Eine sehr wichtige Definition der Winkelfunktionen bezieht sich auf die Verhältnisse der Längen verschiedener Seiten eines rechtwinkligen Dreiecks zu dessen Winkeln. Vom Winkel Alpha

Beschrieben werden die wichtigsten Winkelfunktionen und Rechenregeln im rechtwinkligen Dreieck.

Hier lernst du, wie du die Katheten eines rechtwinkligen Dreieck bestimmst und wofür dies wichtig ist. Hier mehr erfahren!

Du willst wissen, was Winkelfunktionen sind und wie du rechtwinklige Dreiecke mit Winkelfunktionen berechnen kannst? Das alles erfährst du hier im Artikel und in unserem Video !

6.2. Winkelfunktionen (a) Definition Durch Angabe zweier Seiten eines rechtwinkligen Dreiecks ist nach dem Pythagoräischem Lehrsatz auch die dritte Seite eindeutig bestimmt. Sind aber alle

Dreiecksrechner: Berechnungen online am rechtwinkligen Dreieck. Einfach Seite, Winkel, Höhe, p, q eingeben und das gesamte Dreieck mit fehlenden Angaben wird sofort berechnet.

Winkelfunktionen am rechtwinkligen Dreieck. Chapter; pp 253–282; Cite this chapter

Das sind die Formeln der 3 Winkelfunktionen in der Mathematik, die du am besten auswendig lernst. Teste kostenlos unser Selbst-Lernportal . Über 700 Lerntexte & Videos; Über 250.000

Die Winkelfunktionen sind fundamentale mathematische Konzepte, die besonders im rechtwinkligen Dreieck ihre Anwendung finden. Die drei wichtigsten Winkelfunktionen sind

130 Lehrbuchreihen sowie über 40.000 digitale und analoge Zusatzmaterialien machen uns zum führenden Bildungsanbieter in Österreich. Winkelfunktionen im rechtwinkligen Dreieck

Der Kehrwert des Tangens eines Winkels α heißt der Kotangens von α (kurz: cot α). der Kotangens des Winkels α ist gleich dem Tangens des Winkels β. Unter Verwendung spezieller

In diesem Video erkläre ich wie man mit dem Sinus, Kosinus und Tangens in Körpern und im Raum Winkelgrößen und Seitenlängen berechnen kann. Dabei rechne ich 2 Aufgaben vor und

Winkelfunktionen am rechtwinkligen Dreieck Arcusfunktionen im rechtwinkligen Dreieck Einfache Übungsaufgaben lösen können . Lernziele . Winkelfunktionen auf Sachaufgaben anwenden Mit

Strecken und Winkelberechnung mit sin, cos, tan Aufgabe 3: Berechne die fehlenden Dreiecksseiten mithilfe von sin, cos oder tan. Aufgabe 4: Zeichne für das Dreieck ABC eine

Trigonometrie Formeln am rechtwinkligen Dreieck. Damit du aus den gegebenen Größen eines rechtwinkligen Dreiecks die fehlenden Seitenlängen und Winkelgrößen eines Dreiecks berechnen kannst, solltest du die

GORT

Reviews