13.8: More Lagrangian Mechanics Examples

Di: Everly

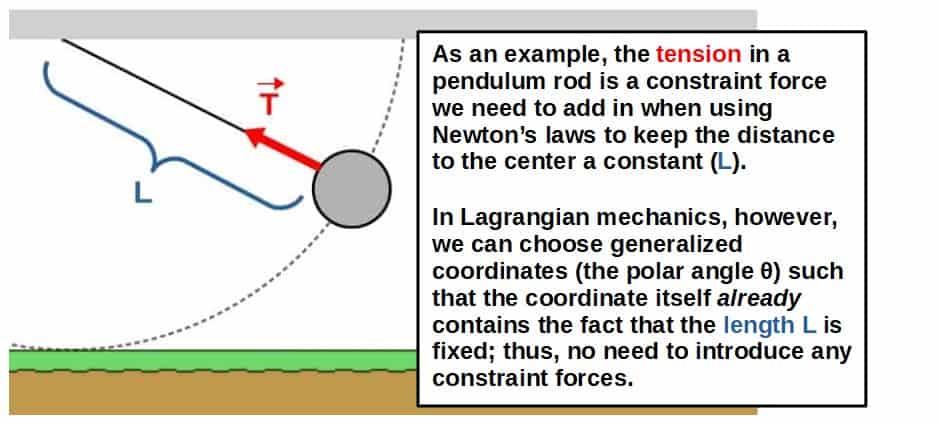
Constraints In Lagrangian Mechanics: A Complete Guide With Examples ...

Non-relativistic Lagrangian and Hamiltonian Mechanics

Classical Mechanics Problem Set 2 ETH Zurich, 2020 HS Prof. N. Beisert, Dr. M. Schiavina 2.1. Galilean group Show that the Galilean transformations (t;~x) 7!(t0;~x0) = ( t+ a;R~x+~vt+~b);

This document provides a solution manual for classical mechanics problems from the textbook „Classical Mechanics“ by J.R. Taylor. It works through solutions to 16 chapters of

Posted by u/[Deleted Account] – 2 votes and 5 comments

Fluids, characterized by a molecular structure that offers no resistance to external shear forces, easily deform even under minimal stress, leading to highly complex and often chaotic dynamics

This page intentionally left blank
Introduction to Classical Mechanics
Chapter 13 Coupled oscillators
Variational Principles Classical Mechanics

• Lagrangian mechanics • Symmetries and conservation laws • Two body systems • Oscillations • Rigid body dynamics • Hamiltonian mechanics • Hamilton-Jacobi equation • Special Relativity

For example, one may wish to relate the inertia tensor through the center of mass to another location that is constrained to remain stationary. 13.9: Perpendicular-axis Theorem for Plane

NDLI: 13.4: The Lagrangian Equations of Motion

This document introduces Lagrangian mechanics as an alternative approach to Newtonian mechanics for solving dynamics problems. [1] Lagrangian mechanics uses generalized

There is an alternative approach known as lagrangian mechanics which enables us to find the equations of motion when the newtonian method is proving difficult. In lagrangian mechanics

Classical Mechanics Systems of Particles and Hamiltonian Dynamics. With a Foreword by D.A. Bromley. Second Edition With 280 Figures, and 167 Worked Examples and Exercises Prof. Dr.

the basic notions of analytical mechanics, but also with some of its main applica-tions: astronomy, statistical mechanics, continuum mechanics and (very brieﬂy) ﬁeld theory. The book has

The Lagrangian Equations of Motion: 13.5: Acceleration Components: 13.6: Slithering Soap in Conical Basin: 13.7: Slithering Soap in Hemispherical Basin: 13.8: More Examples: 13.9:

13.8: More Lagrangian Mechanics Examples 13.9: Hamilton’s Variational Principle 14: Hamiltonian Mechanics 15: Special Relativity 16: Hydrostatics 18: The Catenary 19: The Cycloid 21: Central

Classical Mechanics, John R. Taylor

Contents Contents i List of Figures xiii List of Tables xxi 0.1 Preface

Lagrangian methods are particularly applicable to vibrating systems, and examples of these will be discussed in Chapter 17. These chapters are being written in more or less random order as the spirit moves me, rather than in

Introduction to Classical Mechanics This textbook covers all the standard introductory topics in classical mechanics, including Newton’s laws, oscillations, energy, momentum, angular

giving more emphasis to speciﬁc examples worked out in more detail. Many of the most fascinating recent discoveries about the nature of the Earth and its surroundings — particularly

It represents a generalization of d’Alembert’s principle of classical mechanics to irreversible thermodynamics and leads to equations of evolution of thermodynamic systems.

6.4 More than Two Variables 6.5 Problems for Chapter 6; Lagrange’s Equations 7.1 Lagrange’s Equations for Unconstrained Motion 7.2 Constrained Systems; an Example 7.3 Constrained

Taylor J R Classical Mechanics Solutions1 PDF

Others are more complex, but can still be modeled by two or more masses and two or more springs. Examples include compound mechan-ical systems, oscillating electrical circuits with

Example. Suppose that the initial value of \( \theta\) is \(\alpha\) = 45 o and that we start by pushing the soap horizontally (\( \dot{\theta}=0\)) at an initial angular speed \( \Omega\) = 3 rad

It works through solutions to 16 chapters of mechanics problems, showing calculations and reasoning step-by-step. The document includes solutions to problems

For example, if a bound cluster of stars occupies a spherical volume of uniform density, the potential energy is \(\frac{3GM^{2}}{5a}\) (Equation 5.9.1 of Celestial Mechanics), so the virial theorem (Equation \( \ref{eq:3.13.16}\)) will enable you

This textbook covers all the standard introductory topics in classical mechanics, including Newton’s laws, oscillations, energy, momentum, angular momentum, planetary motion, and

Quantum mechanics has played an important role in photonics, quantum electronics, and micro-electronics. But many more emerging technologies require the

Introduction to Classical Mechanics This textbook covers all the standard introductory topics in classical mechanics, including Newton’s laws, oscillations, energy, momentum, angular

It is one of the more sophisticated elds in physics that has a ected our understanding of nano-meter length scale systems important for chemistry, materials, optics,

elegant and succinct than Newtonian mechanics. More importantly, the concepts in analytical mechanics can be generalized to hyperspace/phase space, in which we do not live. Moreover,

Orbital Mechanics, Second Edition by John E. Prussing and Bruce A. Conway Oxford University Press 2013 Contents Chapter 1 The n – Body Problem 1.1 Introduction, 1 1.2 Equations of

This chapter is intended to introduce the basic notions of the Lagrangian and Hamiltonian formalisms as well as Noether’s theorem. Using this theorem we reveal the

More examples of using Lagrangian Mechanics to solve problems. Hamilton’s variational principle in dynamics is slightly reminiscent of the principle of virtual work in statics. When using the

GORT

Reviews