GORT

Reviews

1 Introduction To Markov Random Fields

Di: Everly

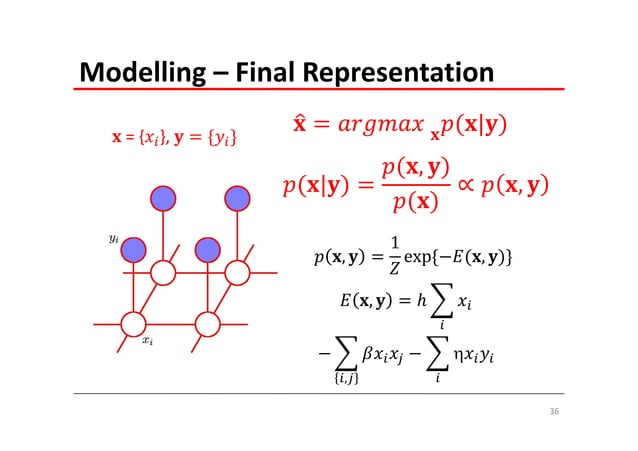
Markov Random Field (MRF)

Hidden variables associated with the nodes are introduced into a model designed to “explain” the values (colors) of all the pixels. A joint probabilistic model is built over the pixel values and the

CRFs are a type of discriminative undirected probabilistic graphical model.. Lafferty, McCallum and Pereira [1] define a CRF on observations and random variables as follows: . Let = (,) be a

Markov Random Fields and Stochastic Image Models

We understand this as saying that the random variable Xv, conditioned on the values of the random variables at the neighboring vertices, is independent of the remaining random variables.

1. Introduction 2. The Bayesian Approach 3. Discrete Models (a) Markov Chains (b) Markov Random Fields (MRF) (c) Simulation (d) Parameter estimation 4. Application of MRF’s to

  • An Introduction to Conditional Random Fields
  • Conditional Random Fields
  • Fast and Differentiable Message Passing on Pairwise Markov Random Fields

– Introduction to MRFs • Today – More MRFs. 2. Markov Random Fields (MRFs) • A Markov random field is an undirected graphical model – Undirected graph ??= (??,??) – One node for each

9.3.4 Gaussian Markov Random Fields. To illustrate possible generalizations of the Markov random fields defined on a finite graph and taking non discrete values, we discuss

Introduction Neighborhoods and cliques De nition of a Markov Random Field Hammersley-Cli ord theorem and conditional probability Sampling MRF (Gibbs, Metropolis) Optimization 2

Multi-parameter processes extend the existing one-parameter theory in an elegant way and have many applications to other fields in mathematics such as real analysis, functional analysis,

In this book we study Markov random functions of several variables.

Markov Random Field (MRF) Markov randomfields were introduced by Besag in 1974. Definition Let YV = [Yi,i∈ V]T denote the random vector of measurements in set V. YV is a

1. Introduction Markov Random Fields (MRFs), also known as undi-rected probabilistic graphical models, are ubiquitous structured probability models that have signi cantly impacted a large

Roughly, a random field with denumerable state space S is described by a probability measure IL on the space Q = ST of all configurations of values from S on the generalized time set T.

1 Introduction Optimization of Markov Random Fields (MRFs) has been a well-studied problem for decades with a significant impact on many computer vision applications such as stereo vision

Conditional Random Fields: An Introduction or Markov random field [3], globally conditioned on X, the random variable representing observation sequences. Formally, we define G = (V,E)

1. An introduction to conditional random fields & Markov random fields. A conditional random field is a discriminative model class that aligns with the prediction tasks in

In this chapter we discuss certain extensions of Markov chains, called Markov fields which have been important objects of study in the recent development of probability theory.

There exist graphical models associated with different kinds of graph structures, for example, factor graphs, Bayesian networks associated with directed graphs, and Markov

Dynamic Bayesian Network is a probabilistic graphical model that represents a sequence of random variables and their conditional dependencies. Markov Chain is a simple Dynamic

This chapter presents an introduction to Markov random fields (MRFs), also known as Markov networks, which are undirected graphical models. We describe how a

Download Citation | Introduction to Markov Random Fields | State-of-the-art research on MRFs, successful MRF applications, and advanced topics for future study. This

Markov Random Fields and Stochastic Image Models.

These results are interesting for their applications as well as for the theory. In establishing them, we found it useful to introduce a general probability model which we have called a random field. In this book we investigate random fields

„Introduction to Markov Random Fields“, Markov Random Fields for Vision and Image Processing, Andrew Blake, Pushmeet Kohli, Carsten Rother Download citation file: Ris (Zotero)

4 An Introduction to Conditional Random Fields for Relational Learning x y x y Figure 1.1 The naive Bayes classifier, as a directed model (left), and as a factor graph (right). 1.2.2

On the method-ological side, substantial progress is associated with the introduction of Markov random fields (MRFs), as a class of parametric models for spatial data (Besag 1974).

An Introduction to Spatial Point Processes and Markov Random Fields Valerie Isham Department of Statistical Science, University College London, Gower Street, London WCIE 6BT, England

An Introduction to Conditional Random Fields By Charles Sutton and Andrew McCallum Contents 1 Introduction 268 1.1 Implementation Details 271 2 Modeling 272 2.1 Graphical Modeling 272

Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu.